Как посчитать площадь — комнаты стены пола потолка

Как рассчитать площадь комнаты – пошаговая инструкция

При расчете площади нужно знать длину, ширину и высоту комнаты

Можно, конечно, заглянуть в техническую документацию дома и посмотреть в ней все нужные характеристики. Но, во-первых, там нередко бывают ошибки, во-вторых, иногда проще вычислить всё самостоятельно, чем найти документы.

Для проведения подсчётов нам понадобятся определённые инструменты, большинство из которых можно запросто найти в каждом доме. А именно:

• рулетка;
• карандаш;
• бумага для записей;
• калькулятор (можно использовать калькулятор, который размещён на нашем сайте);
• трезвость ума и ясность мыслей.

Пол

Чтобы высчитать квадратуру пола в прямоугольной или квадратной комнате, необходимо узнать её длину и ширину.

Проводить замеры лучше у основания стен, а для этого желательно отодвинуть или вынести всю мебель. Но, если такая процедура в ваши планы не входила, можно мерить и по центру. Главное при этом, чтобы воображаемая линия, по которой будет производиться измерение, располагалась под углом в 90° к стене.

После того как данные замеров получены и проверены, их нужно перемножить по формуле , где S — площадь в квадратных метрах, a и b — длина и ширина, соответственно.

Если к основному помещению прилегает ниша или какое-нибудь другое — его площадь необходимо вычислить по тому же алгоритму, и результаты приплюсовать к площади комнаты. Если есть различные выступы, которые занимают его часть — их также следует измерить и полученный результат вычесть из общего.

С квадратами и прямоугольниками всё просто. А как посчитать S комнаты, если она имеет неправильную форму? Здесь придётся применить логическое мышление, и немного вспомнить школьный курс алгебры и геометрии. Но давайте по порядку.

Если помещение неправильной формы

Постарайтесь мысленно или на бумаге разделить комнату на простые элементы (квадраты, прямоугольники, треугольники). Далее, нужно будет высчитать размеры каждого из них, и результаты сложить.

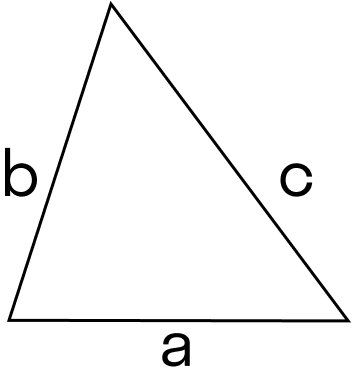
• для треугольника — . Где a — длинна основания треугольника, b — высота, проведённая от вершины к основанию;
• для круга — . Где 3,14, r — радиус круга (чтобы узнать радиус — найдите с помощью рулетки самое длинное расстояние между стенами и разделите его на 2);
• для полукруга — (буквенные обозначения совпадают с предыдущим пунктом).

Как оказалось, и в таком случае ничего сложного нет. Главное, тщательно проверять результаты замеров, чтобы в расчёты не закралась случайная ошибка, и их не пришлось производить заново.

И ещё. Если вы хотите произвести монтаж тёплого пола, не забудьте отдельно вычислить площадь, которую занимает мебель, и вычтите её из общего значения для помещения.

С полом мы разобрались. Но при подготовке, допустим, к переклеиванию обоев это вам мало чем поможет. Нужно будет узнать точное количество квадратных метров, которое занимают  стены.

Стены

Площадь каждой отдельно взятой стены можно высчитать так же, как и квадратуру пола. Только теперь вместо ширины помещения нужно будет измерить её высоту. Множим длину стены на высоту и получаем необходимый нам результат в квадратных метрах.

Измерение высоты лазерной рулеткой

А можно вычислить и для всех стен сразу. Для этого вам понадобится узнать периметр пространства. Возьмите рулетку и измерьте длину каждой стены, результаты сложите — это и будет периметр. Остаётся измерить высоту комнаты и воспользоваться следующей формулой: , где p — периметр, а h — высота.

Теперь необходимо разобраться с оконными, дверными и прочими проёмами, присутствующими в помещении.

Точнее, рассчитать площадь каждого из них (по формулам, представленным выше, в зависимости от формы проёма), результаты суммировать и вычесть из общего количества.

Существует также ряд общих рекомендаций по проведению замеров.

Площадь стен со сложной поверхностью

Нередко в помещениях много разных элементов, которые усложняют подсчет площади. Так что если стены не прямоугольные или есть разные дополнительные детали, необходимо воспользоваться иным способом расчета площади дома.

1. Площадь стен дома с вычетом дверей и окон.

Двери и окна обычно вычитают из общей площади, потому что на них не идет расход материала. Но как посчитать площадь стен без них?

Для начала замеряется ширина и высота окон и дверей.

Формула для площади поверхности – S = a x h.

Если ширина окна 1 м, а высота 1,5 м, то S = 1 х 1,5 = 1,5 м².  При ширине двери 0,9 м и высоте в 2 м получаем S = 0,9 х 2 = 1,8 м². Теперь нужно отнять от общей площади, площадь окон, дверей и получается площадь без них. То есть,

S стен = 66 – 1,5 – 1,8 = 62,7 м² (если использовать площадь стен, полученную в предыдущем пункте).

1. Если комната нестандартной конструкции.

Когда помещение имеет нестандартную форму, расчет площади стен проводится немного иначе. Сначала считается площадь каждой стены в отдельности.

S = a x b, где, а – ширина стены, b – высота стены.

Если есть колонны, выступы, их площадь также измеряется, а затем все эти площади суммируются. То есть, итоговая формула это S = S1 + S2 + S3 + S4 и т. д.

Важно!
В редких случаях геометрические параметры стен абсолютно правильные. Так что для наиболее точных расчетов стоит делать измерения в нескольких местах, а потом выводить среднее арифметическое число и уже его использовать в формулах.

1. Если имеются круглые элементы в архитектуре.

Помещения с круглыми или полукруглыми стенами это не редкость. Чтобы просчитать их площадь используется другая формула. Первым делом вымеряется их периметр. Для этого нужно умножить диаметр на 3,14 (число Пи, π). А затем уже подсчитывается и площадь по формуле:

S = P x h, где, h – это высота.

Когда нужно вычесть из общей квадратуры площадь круглых объектов, нужно рассчитать площадь круглых поверхностей и просто отнять их. Но, если нет возможности вымерять диаметр или радиус, то вымеряют длину окружности (P) и считают площадь, применяя формулу S = P² / 4 π.

1. Площадь с треугольными элементами.

Треугольные стены могут быть, к примеру, на чердаке или в случае, когда используются сложные конструкции на потолке или архитектурные украшения на стенах. В зависимости от типа треугольника использовать можно разные формулы.

• Разносторонний треугольник: S = , где, а – основа треугольника – нижняя сторона, а h – высота от пола к верхнему углу.
• Прямоугольный треугольник: S = , где, а – высота треугольника, а b – нижняя, горизонтальная сторона.
• Равносторонний треугольник (правильный): S = , где, а – сторона треугольника.

По радиусу описанной окружности и стороне

Можно просто найти диаметр (умножить радиус на два) и использовать формулу выше.

Другой способ:

1. Найти квадрат радиуса (умножьте радиус на радиус).
2. Умножить квадрат радиуса на 4.
3. Найти квадрат известной стороны.
4. Отнять от четырех радиусов в квадрате квадрат известной стороны (из второго отнять третье).
5. Найти квадратный корень разности.
6. Умножить корень на известную сторону.

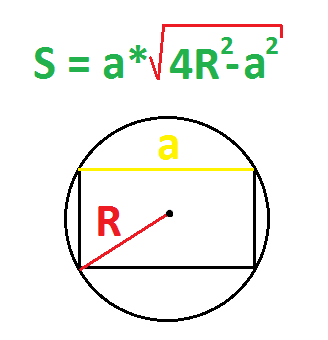
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 5 см, а одна из сторон равна 6 см.

1. Квадрат радиуса: 5*5=25 см.
2. Четыре квадрата радиуса: 4*25 = 100 см.
3. Квадрат стороны: 6*6 = 36 см.
4. Отнимаю от четырех радиусов в квадрате квадрат стороны: 100-36 = 64 см.
5. Нахожу квадратный корень разности. Корень из 64 равен 8 см.
6. Умножаю корень на сторону: 8*6 = 48 см.

Ответ: 48 см.

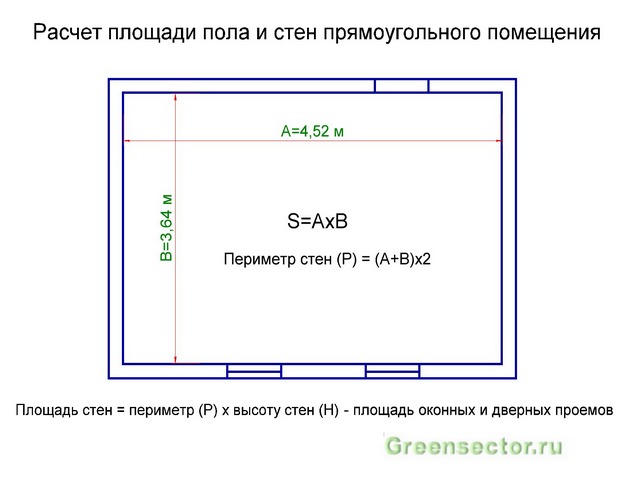
Вычисление площади прямоугольной комнаты

Помещение, не имеющее никаких, даже небольших, выступов и ниш или, попросту говоря, прямоугольное – самый простой вариант для снятия мерок и подсчета значений площади. Здесь достаточно вспомнить самую простую формулу из курса математики – как рассчитывается площадь такой фигуры, как прямоугольник. Для этого необходимо измерить лишь ширину (А) и длину комнаты (B). Таким образом, мы получаем, что S (площадь) будет равна значению, которое будет получено в результате перемножения двух показателей А и В.

Расчет площади прямоугольной комнаты

Результаты всех измерений указываются в метрах. После запятой указываются сантиметры. Например, длина стены получилась 376 см, тогда получается (в 1 м – 100 см), что длина этой стены будет равна 3 м 76 см.

Меряем прямоугольный пол

Если в комнате есть камин, то нужно посчитать его площадь и отнять от получившейся цифры. Ведь под камином напольное покрытие укладываться не будет. Конечно, если речь не идет о демонтаже этого сооружения.

Для равнобедренного треугольника

Рассмотрим случаи нахождения площади, если у треугольника равные боковые стороны.

Через основание и сторону

 В этом случае формула будет выглядеть следующим образом:

\(S=\frac b4\sqrt{4a^2-b^2}\)

где a — одно из боковых ребер фигуры, а b — ее основание.

Через основание и противолежащий угол

Зная длину основания и противолежащий ему угол, мы можем использовать следующую формулу:

\(S=\frac{b^2}{4\tan\left({\displaystyle\frac\beta2}\right)}\)

где b — основание многоугольника, β — противолежащий ему угол.

Через основание и высоту

Если нам известна величина основания равнобедренного треугольника, а также его высота, найдем S по приведенной ниже по элементарной формуле:

\(S=\frac{b\times h}2\)

где b — основание фигуры, а h — высота, проведенная к этому основанию.

Через боковые стороны и угол между ними

Если мы знаем длину боковых сторон и угол между ними, найдем площадь, опираясь на расчеты:

\(S=\frac12a^2\times\sin\left(\beta\right)\)

где a — это боковое ребро, β — угол между равными ребрами.

Через основание и угол между боковыми сторонами

В этом случае нам сначала придется найти высоту по формуле:

\(h=\frac b2\tan\left(\beta\right)\)

где β — угол при вершине, а b — основание.

Далее подставляем значение в формулу

\(S=\frac{b\times h}2 = \frac{b\times{\displaystyle\frac b2}\tan\left(\beta\right)}2=\frac{b^2\tan\left(\beta\right)}4\)

Итоговая формула:

\(S=frac{b^2\tan\left(\beta\right)}4\)

Как рассчитать площадь комнаты — задача для первоклассников

Что может быть про­ще рас­че­та пло­ща­ди пря­мо­уголь­ни­ка? Ведь это самая пер­вая и про­стая зада­ча из учеб­ни­ка гео­мет­рии для пер­во­го класса.

• Изме­ре­ние про­во­дим при помо­щи стро­и­тель­ной рулет­ки с фик­са­то­ром, жела­тель­но у плин­ту­сов, так как если будем делать это посре­дине ком­на­ты, может полу­чить­ся погреш­ность. Жела­тель­но при­сут­ствие помощ­ни­ка, кото­рый будет при­дер­жи­вать один конец рулет­ки. В про­тив­ном слу­чае мож­но закре­пить её каким-то тяжё­лым пред­ме­том или заце­пить за край плинтуса.
• Если дли­на изме­ря­ю­щей лен­ты недо­ста­точ­на, замер при­дёт­ся про­во­дить поэтап­но, фик­си­руя лен­ту и про­став­ляя мет­ки. Затем сум­ми­ру­ем участ­ки дли­ны по про­став­лен­ным мет­кам и полу­ча­ем общий размер.

Напри­мер, дли­на ком­на­ты 5 м, а шири­на — 4 м. Пере­мно­жим эти две циф­ры, полу­ча­ем пло­щадь ком­на­ты — 20 м2 .

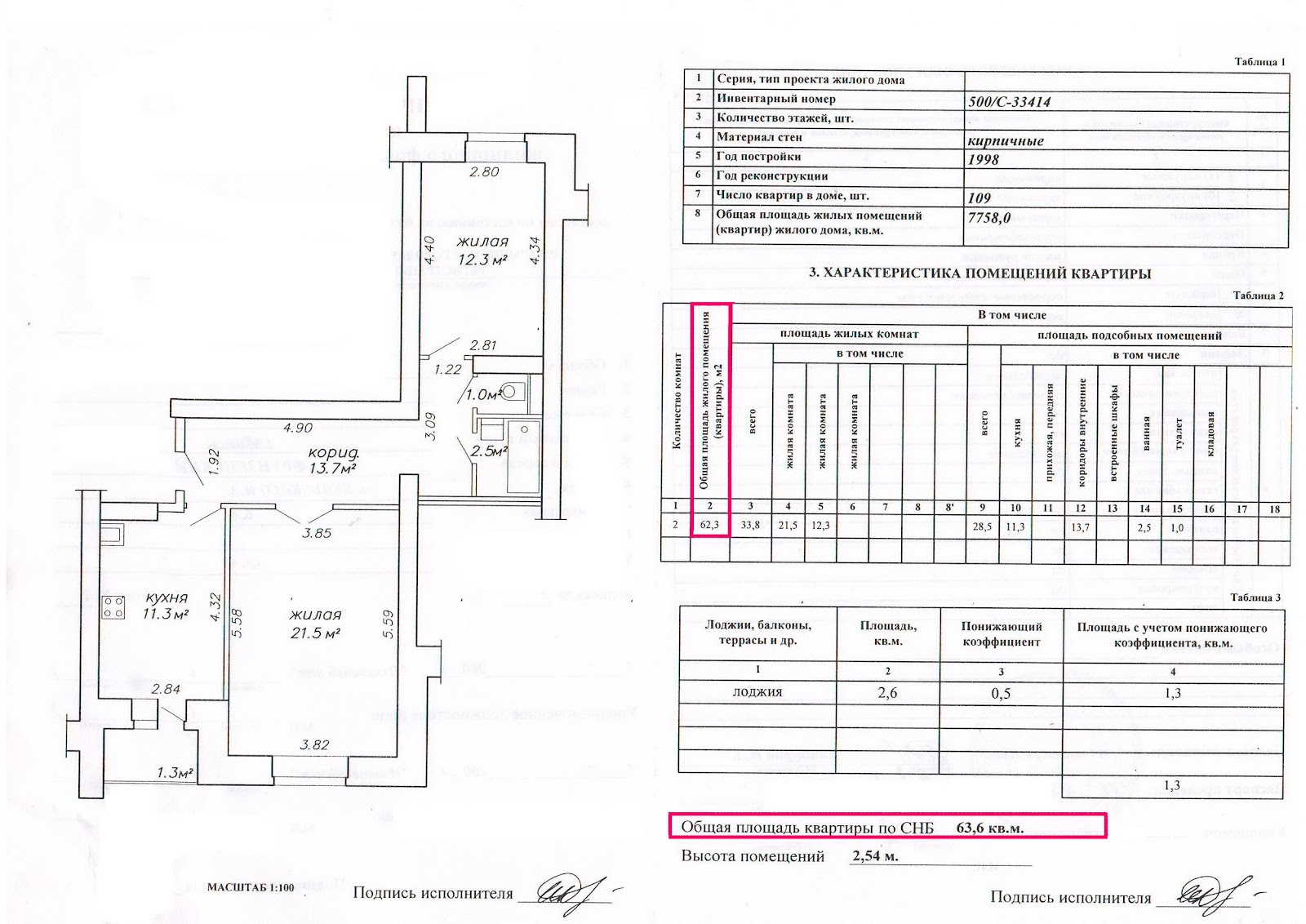
Как измерить площадь помещения с нишей

Услож­ним зада­чу: допу­стим в поме­ще­нии име­ет­ся пря­мо­уголь­ная ниша. В этом слу­чае раз­би­ва­ем ком­на­ту на два пря­мо­уголь­ни­ка боль­шой и малень­кий. Изме­рить нуж­но будет две сто­ро­ны боль­шо­го и две сто­ро­ны малень­ко­го прямоугольника:

• дли­ну мень­шей сто­ро­ны ком­на­ты (рас­сто­я­ние до ниши) а1;
• шири­ну ком­на­ты — b1;
• дли­ну и шири­ну ниши а2 и b2 .

Пло­щадь ком­на­ты будет рав­но сум­ме най­ден­ных пло­ща­дей двух пря­мо­уголь­ни­ков: S = а1* b1   + а2 * b2.

Рас­счи­та­ем пло­щадь ком­на­ты на рисун­ке ниже.

Здесь: а1 = 4.35 м; b1 = 5 м; а2 = 2.65 м; b2 = 2.5 м.

S = 4.35 * 5 + 2.65 * 2.5 =21.75 +6.625 = 28.375 м2.

Как рассчитать площадь комнаты любой формы

Прин­цип рас­че­та оди­на­ков для поме­ще­ний любой формы:

Для вычис­ле­ний доста­точ­но знать сле­ду­ю­щие формулы:

• S пря­мо­уголь­ни­ка = a * b (1), здесь и далее а и b — дли­на и шири­на помещения.
• S пря­мо­уголь­но­го тре­уголь­ни­ка (это поло­ви­на пря­мо­уголь­ни­ка), то есть S тре­уг. = a * b /2 (2);
• S кру­га = π*r2 (или π*d2 / 4) (3) , где π = 3.14, r и d — ради­ус и диа­метр окружности;
• S полу­кру­га = π*r2 /2 (4);
• S тра­пе­ции с осно­ва­ни­я­ми а, b и высо­той h: S трап. = (а + b)/2 * h (5).

Как рассчитать квадратуру стен

Определение площади стен часто требуется при закупке отделочных материалов — обоев, штукатурки и т.п. Для этого расчета нужны дополнительные измерения. К имеющимся уже ширине и длине комнаты нужны будут:

• высота потолков;
• высота и ширина дверных проемов;
• высота и ширина оконных проемов.

Все измерения — в метрах, так как квадратуру стен тоже принято измерять в квадратных метрах.

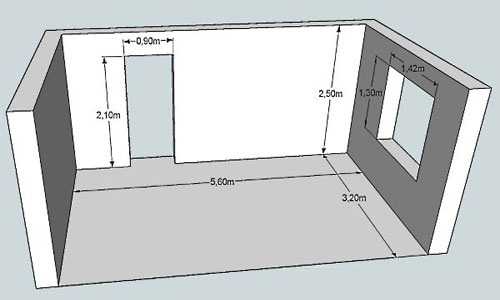
Удобнее всего размеры наносить на план

Так как стены прямоугольные, то и площадь считается как для прямоугольника: длину умножаем на ширину. Таким же образом вычисляем размеры окон и дверных проемов, их габариты вычитаем. Для примера рассчитаем площадь стен, изображенных на схеме выше.

1. Стена с дверью:
   • 2,5 м * 5,6 м = 14 кв. м. — общая площадь длинной стены
   • сколько занимает дверной проем: 2,1 м *0,9 м = 1,89 кв.м.
   • стена без учета дверного проема — 14 кв.м — 1,89 кв. м = 12,11 кв. м
2. Стена с окном:
   1. квадратура маленьких стен: 2,5 м * 3,2 м = 8 кв.м.
   2. сколько занимает окно: 1,3 м * 1,42 м = 1,846 кв. м, округляем, получаем 1,85 кв.м.
   3. стена без оконного проема: 8 кв. м — 1,75 кв.м = 6,25 кв.м.

Найти общую площадь стен не составит труда. Складываем все четыре цифры: 14 кв.м + 12,11 кв.м. + 8 кв.м + 6,25 кв.м. = 40,36 кв. м.

Общая формула

S = 0,5 * a * b⋅sin(α) , где a, b — стороны, α — угол между ними.

S = 0,5 * a * h, где a — основание, h — высота.

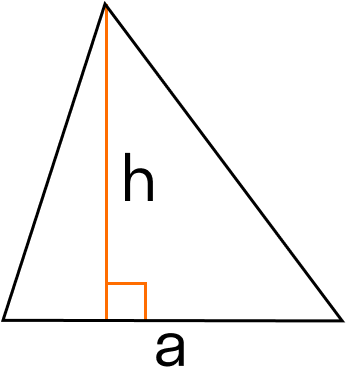
S = (a * b * c) : (4 * R), где a, b, c — стороны, R — радиус описанной окружности.

4. Площадь треугольника через вписанную окружность и стороны.

S = r * (a + b + c) : 2, где a, b, c — стороны, r — радиус вписанной окружности.

Если учитывать, что (a + b + c) : 2 — это способ поиска полупериметра. Тогда формулу можно записать следующим образом:

S = r * p, где p — полупериметр.

S = a2 : 2 * (sin(α)⋅sin(β)) : sin(180 — (α + β)), где a — сторона, α и β — прилежащие углы, γ — противолежащий угол.

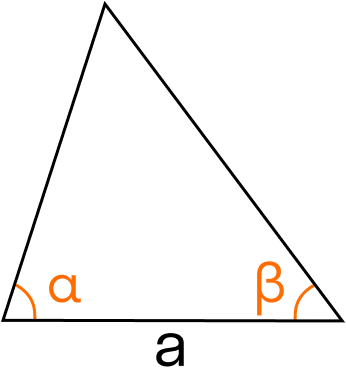
6. Формула Герона для вычисления площади треугольника.

Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.

S = √ p * (p − a) * (p − b) * (p − c)​, где a, b, c — стороны, p — полупериметр, который можно найти по формуле: p = (a + b + c) : 2

Определение площади

Существует несколько способов такого определения площади участков земли:

Наиболее точным из этих методов является аналитический. Это связано с тем, что при его использовании на точность результатов влияют только ошибки полевых измерений, тогда как на два других метода оказывают влияние ошибки плана или карты, с которых снимаются данные.

Расчет площади аналитическим методом

При использовании аналитического способа площадь определяется по данным полевых измерений или по координатам поворотных точек, являющихся функциями результатов полевых измерений.

Участки имеют разные геометрические формы. В частности, они могут иметь четырехугольную форму.

Такая форма участка часто существует в старых садоводческих товариществах, в которых нарезались участки в 6 соток.

Если участок имеет форму трапеции и известны основные параметры такой фигуры, то площадь участка может быть рассчитана по формуле:

• a и b — основания фигуры,
• h – высота трапеции.

Если известны координаты поворотных точек , то площадь надела может быть определена по приведенной ниже общей формуле для многоугольника. При этом для трапеции расчет площади производится по формуле с учетом того, что n=4.

При расчете четырехугольника неправильной формы, когда известны величины каждой из его сторон, необходимо определить величину периметра 2p:

a,b,c,d — величины сторон.

Тогда площадь участка Sнф будет равна:

В формуле используется значение половины периметра p.

Если участок имеет форму многоугольника с n сторонами, то его площадь рассчитывается по координатам поворотных точек:

• Xi и Yi — координаты i-той поворотной точки участка, имеющего вид многоугольника,
• i — порядковый номер точки. Этот параметр меняется от 1 до n,
• n — число характерных точек.

Для проверки правильности расчетов используется другая формула:

Если расчеты проведены правильно, то Sу1 = Sу.

В этом случае аналитический расчет площади участка производится с использованием данных об углах азимута. При этом по контуру границ участка производится замер азимута каждой поворотной точки. Также определяется расстояние от одной точки до следующей за ней точки. Вся эта информация в дальнейшем вводится в ЭВМ, которая по специальной программе производит расчет площади земельного надела.

Налог при сдаче квартиры в аренду — это тема нашего подробного материала!

Как быстро получить комнату в общежитии и кто из жильцов имеет на это полное право? Узнайте всю необходимую вам информацию в нашей статье.

Хотите безопасно оплатить покупку квартиру и не пострадать от мошенников? Наша статья вам поможет!

Зачем проводить расчет площади комнаты?

Любой ремонт не может начинаться без точных знаний о размерах комнаты. Чтобы посчитать количество обоев или панелей, нужно узнать размеры и площадь стен, для приобретения достаточного количества потолочной плитки снимаются мерки с потолка. Конечно, для закупки в требуемых объемах напольного покрытия также придется постараться и узнать значение площади всего пространства пола.

Для чего могут пригодится расчеты площади

Со снятием мерок с помещения и определением площади основания сталкивается каждый человек, который решил самостоятельно начать ремонт. Если владелец жилого помещения обратился за помощь к специалистам, то ему ни во что вникать не придется – мастера все сделают сами. Однако все же многие решаются на проведение ремонтных работ своими руками. Это позволяет значительно сэкономить деньги, затраченные на ремонт.

Для ремонта необходимо точно знать размеры комнаты

Основные причины необходимости определения площади пола следующие:

• ремонт или первичная укладка напольного покрытия;
• заливка свежей стяжки;
• обустройство системы лаг;
• окрашивание пола;
• нанесение на пол других строительных материалов;
• определение размера жилой площади при оформлении документов либо покупке/продаже квартиры или дома;
• определение соответствия помещения плану комнат;
• подбор мебели по габаритам;
• составление плана комнаты для проведения дальнейших работ;
• оценка стоимости работы специалистов и других затрат.

Не всегда измерение площади пола оказывается простой процедурой

В основном, знание площади пола требуется для того, чтобы высчитать нужное для отделки количество строительных материалов, которые будут использованы при работе. Например, объем цементной смеси для заливки стяжки, количество наливного пола или пачек ламината и т. д.

Виды напольного покрытия

Как подготовиться к расчетам

Проведение подготовительных манипуляций заключается в подготовке места для измерений. Также необходимо подготовить инструмент и специальные принадлежности. Лучше если комната будет свободной от посторонних предметов. Часто такое случается при замерах в новом доме или во время проведения ремонта. Замеры длины сторон производятся вдоль стенок. При этом нужно освободить хотя-бы участки, для свободного проведения рулеткой. Результаты замеров можно сразу же перенести на схему. Обязательно следует проверить прямоугольности комнаты. Для этого выполняется замер диагональных линий.

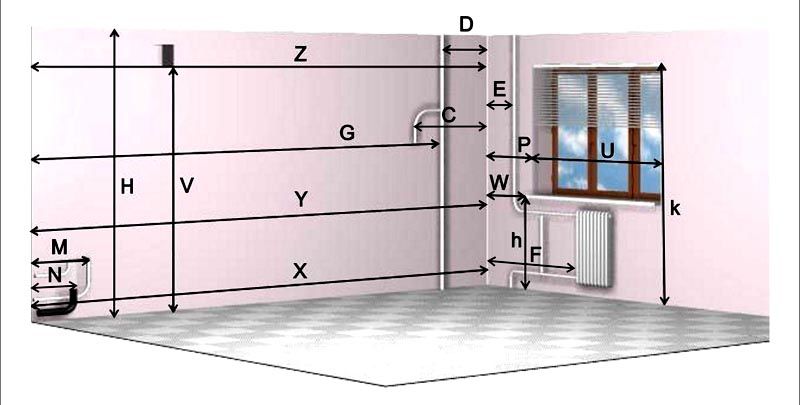Особенности замеров с учетом линий коммуникаций

Кроме рулетки вам может понадобиться специальная линейка для проверки прямых линий. Это может быть строительный уровень или правило. Иногда необходим строительный угольник больших размеров. Как вариант, самодельный циркуль. Можно использовать кусок шнура, привязанный к острому штырю. Для пола можно использовать специальные принадлежности для замеров. Для этого подойдет маркер, мел или скотч. Замеры выполняйте несколько раз. Это позволит избежать ошибки. Следите, чтобы лента для проведения замеров не провисала. Помните, что на многие измерительные инструменты наносится две шкалы. Нельзя путать метрическую систему и дюймовую.

Лазерное приспособление заметно облегчает работу

Перед замерами набросайте простой план – схему на бумаге. Это позволит правильно распределить все замеры. Стоит учитывать, что многие формулы расчетов очень сложные. В этом случае посчитать в столбик не получится. Чтобы посчитать без ошибок, можно воспользоваться программой Excel.

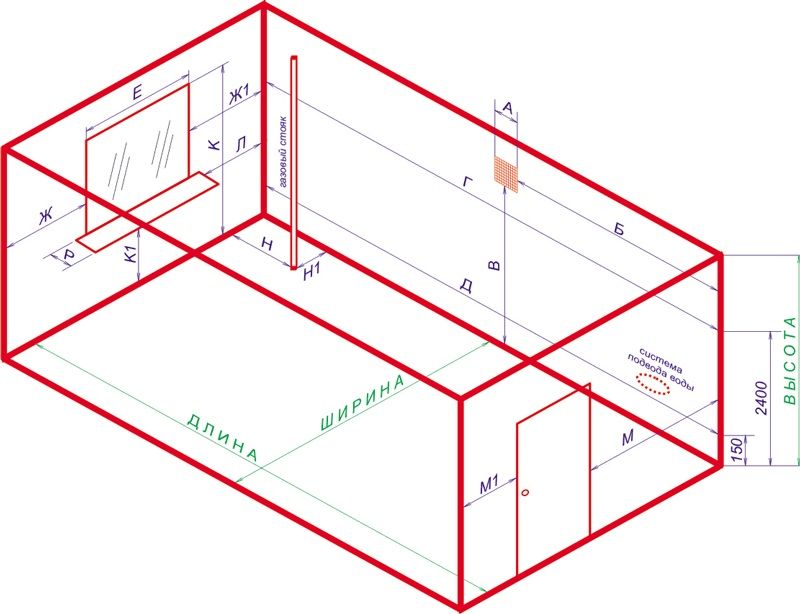На схеме показаны все необходимые замеры для правильных расчетов

Расчет площади стен

Онлайн-калькулятор, который есть на многих специализированных сайтах, дает возможность практически моментально осуществить расчет поверхности стен. Считать эту величину нужно для того, чтобы расчитать необходимое количество обоев, краски, замазки и прочего стройматериала. С помощью онлайн-калькулятора можно подсчитать не только квадратуру, но и количество обоев, необходимых в данном случае и т. д.

Онлайн калькулятор — очень удобный инструмент для расчета площади стен, но и для него нужно знать некоторые параметры:

• длину комнаты;
• ширину;
• высоту.

Но если в данный момент калькулятор в Интернете недоступен, то рассчитать кв. метры поверхности стен можно по формуле:

S = Р х С, где:

S — площадь стен

Р — периметр комнаты

С — высота стен.

Р = (А + В) х 2, где:

B — ширина.

Для того, чтобы максимально точно вычислить поверхность стен в квадратных метрах, нужно из полученного общего результата площади стен вычесть квадратуру дверных и оконных проемов. При этом нужно учитывать, что метраж стен комнат с выступами или углублениями отличаться от аналогичного параметра простой комнаты не на один кв. метр. Поэтому нужно к основному значению прибавлять каждый квадратный метр выступа или углубленного участка.

Кроме того, измерять и рассчитывать нужно с учетом того, что разного типа рулетки могут давать разные результаты, если их неправильно использовать. Точнее всего измеряет обычный метр, которым пользовались еще в советские годы. Например, чтобы измерить квадратуру стен с использованием лазерной рулетки, нужно следить за тем, чтобы ее луч направлялся строго перпендикулярно стенам, иначе может получиться большая погрешность в результатах, отличающаяся от действительности далеко не на один метр.

Перед тем как высчитать площадь комнаты, следует ее освободить от мебели. Но если это невозможно, то ее нужно просто отодвинуть и только после этого измерить длину и ширину у основания стены. Но есть еще один вариант того, как посчитать площадь пола, не трогая и не передвигая мебель.

Оказывается, измерить можно и по центру помещения. При этом необходимо, чтобы воображаемая линия, по которой предстоит вычислить квадратуру комнаты, располагалась бы под прямым углом к стене. Причем, нужно учитывать и то, что считать нужно в одной величине — в квадратных сантиметрах или метрах, а в конце, если пришлось считать в сантиметрах, перевести их в квадратный метр.

Для того чтобы получить точный метраж стен, опытные строители рекомендуют измерять стены в трех местах — в начале, конце и в середине. После этого полученные результаты, используя калькулятор, нужно просуммировать и поделить на три: таким образом высчитывается среднее арифметическое значение. Подобная процедура поможет избежать погрешностей, даже если стены в комнате далеко не самые ровные.

В случае пола в прямоугольной или квадратной комнате правильнее собственноручно измерить все четыре стороны комнаты, а не только две соприкасающиеся. Это обезопасит владельца от последствий халатности строителей дома и от лишних затрат, к примеру, при установке плинтуса.

Если рулеточный метр не фиксируется, то нужно попросить другого человека встать у другого конца стены, чтобы контролировать его край, причем, нужно быть внимательным, чтобы конец метра находился бы точно в углу, непосредственно у края стены.

Сложив квадратуры всех комнат, в итоге можно получить полный метраж квартиры. При этом считать нужно внимательно, используя калькулятор, поскольку в случае ошибки весь процесс измерения окажется напрасным.

Кому-то, конечно, может показаться смешным «школьный» вопрос о том, как можно точно рассчитать квадратуру какого-либо помещения, но ведь многие из тех, кто его задает, уже давно кончали школу и, вполне вероятно, очень давно не проводили каких-либо математических подсчетов, которые волею судьбы им были просто не нужны.

К тому же многие помещения в доме могут быть нестандартной формы, поэтому чтобы посчитать их метраж, человеку придется проявить немалую сообразительность, чтобы максимально облегчить свою работу.

Обсуждение закрыто.

Свойство аддитивности площади

Предположим, что нам надо найти площадь прямоугольника со сторонами 2 и 1. Его можно разбить на два квадрата со стороной 1, то есть на два единичных квадрата:

Этот прямоугольник занимает на плоскости в два раза больше места, чем единичный квадрат, поэтому логично считать, что его площадь равна 2. В данном случае мы разбили многоугольник на две фигуры, площадь каждой из которых нам была известна. Далее мы сложили площади известные нам площади и получили площадь прямоугольника.

В общем случае справедливо утверждение, что площадь всякой фигуры равна сумме площадей фигур, из которых она может быть составлена. Это свойство называют аддитивностью площади:

Площадь – не единственная величина, обладающая свойством аддитивности. Например, длина любого отрезка равна сумме длин отрезков, из которых он состоит. В классической физике считается, что масса сложного тела равна сумме масс тел, составляющих его. Аддитивность можно считать основным свойством площади.

Свойство аддитивности подсказывает нам, как измерять площадь произвольных многоугольников. Достаточно разбить такой многоугольник на несколько фигур, чья площадь нам известна, и сложить их площади.

Задание. Найдите площадь фигуры, показанной на рисунке. Длина стороны одной клеточки равна единице.

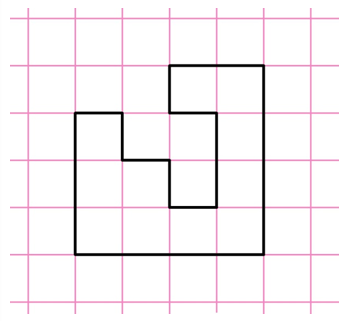
Решение. Каждая клеточка является, по сути, единичным квадратом, чья площадь равна 1. Можно видеть, что нарисованная фигура состоит 11 таких квадратов:

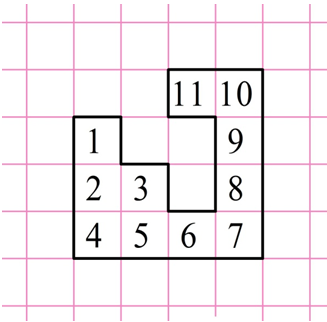
В силу свойства аддитивности площадь фигуры равна сумме площадей этих квадратов:

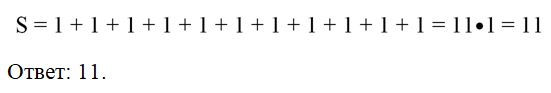
Если две фигуры можно разбить на одинаковые фигуры, то их называют равносоставленными фигурами. Покажем пример равносоставленных фигур, которые состоят из двух половинок круга:

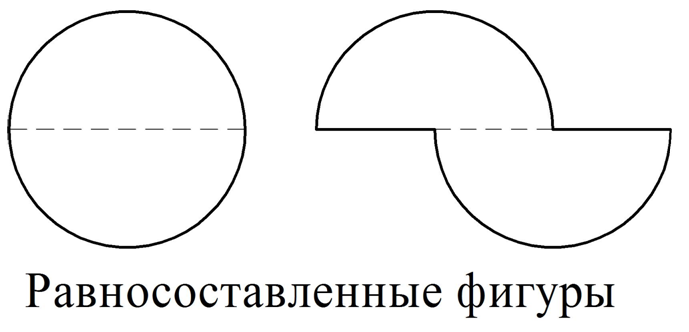
Довольно очевидно, что равносоставленные фигуры имеют равную площадь. Также очевидно, что любые две равные фигуры являются равносоставленными, а потому их площади тоже равны.

Важно понимать разницу между равными и равносоставленными фигурами. Фигуры равны, если их можно наложить друг на друга, и при этом они полностью совпадут

Равносоставленные же фигуры могут и не накладываться друг на друга.

Ещё одно важное понятие – равновеликие фигуры. Так называют фигуры, чьи площади равны

Мы уже сказали, что любые две равносоставленные фигуры имеют одинаковую площадь, то есть являются равновеликими. Верно ли обратное? Всякие ли равновеликие фигуры являются равносоставленными? Оказывается, что нет. Можно нарисовать окружность и квадрат, имеющие равные площади, но разбить их на одинаковые фигуры не получится:

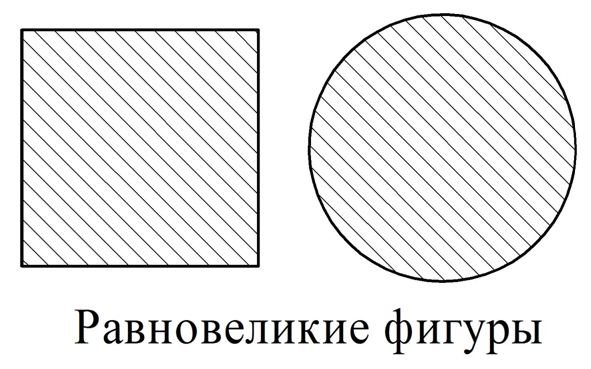
С помощью равных и равновеликих фигур можно находить площади фигур, которые невозможно разбить на единичные квадраты.

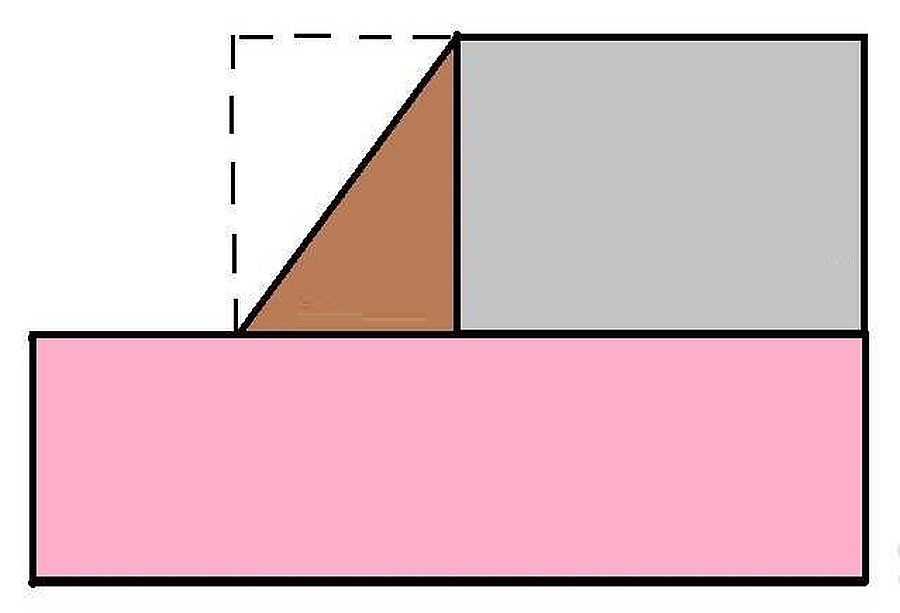
Задание. Найдите площадь прямоугольного треугольника, катеты которого равны единице.

Решение. Достроим такой прямоугольник до единичного квадрата. В результате гипотенуза треугольника окажется диагональю квадрата:

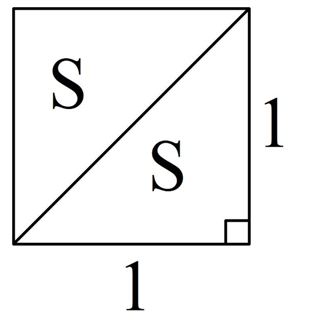
Получили, что единичный квадрат состоит из двух равных треугольников, чью площадь нам и надо найти. Обозначим площадь треугольника как S. Тогда справедливо равенство

Итак, зная свойства площади фигур, мы попытаемся дать этому понятию определение. Можно сказать, что площадь – это число, характеризующее плоскую фигуру и имеющее следующие свойства:

• площадь квадрата со стороной 1 равна единице:
• равносоставленные фигуры имеют равную площадь.

Такого описания вполне достаточно, чтобы вывести все формулы для нахождения площади многоугольников.