Как посчитать площадь треугольника

Как подготовиться к расчетам

Проведение подготовительных манипуляций заключается в подготовке места для измерений. Также необходимо подготовить инструмент и специальные принадлежности. Лучше если комната будет свободной от посторонних предметов. Часто такое случается при замерах в новом доме или во время проведения ремонта. Замеры длины сторон производятся вдоль стенок. При этом нужно освободить хотя-бы участки, для свободного проведения рулеткой. Результаты замеров можно сразу же перенести на схему. Обязательно следует проверить прямоугольности комнаты. Для этого выполняется замер диагональных линий.

Кроме рулетки вам может понадобиться специальная линейка для проверки прямых линий. Это может быть строительный уровень или правило. Иногда необходим строительный угольник больших размеров. Как вариант, самодельный циркуль. Можно использовать кусок шнура, привязанный к острому штырю. Для пола можно использовать специальные принадлежности для замеров. Для этого подойдет маркер, мел или скотч. Замеры выполняйте несколько раз.
Это позволит избежать ошибки. Следите, чтобы лента для проведения замеров не провисала. Помните, что на многие измерительные инструменты наносится две шкалы. Нельзя путать метрическую систему и дюймовую.

Перед замерами набросайте простой план – схему на бумаге. Это позволит правильно распределить все замеры. Стоит учитывать, что многие формулы расчетов очень сложные. В этом случае посчитать в столбик не получится. Чтобы посчитать без ошибок, можно воспользоваться программой Excel.

Расчет площади пола в комнате неправильной формы

У комнат, имеющих неправильную форму, рассчитать площадь намного сложнее. Сложности добавляют такие элементы, как арки, ниши в форме полукруга, скошенные стены и т. д. По сути, принцип расчета тот же – нужно разбить помещение на несколько ровных фигур и высчитать площадь каждой отдельно, а потом суммировать. Но площадь круга или треугольника считается уже по другим формулам.

Пол неправильной формы

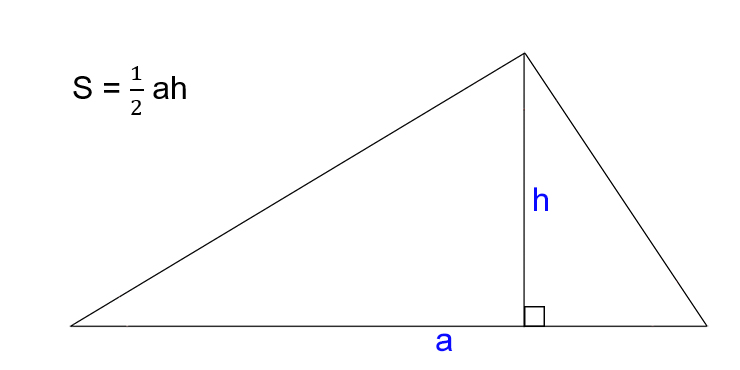
Например, площадь треугольника высчитывается так: длина основания умножается на высоту треугольника и делится на 2.

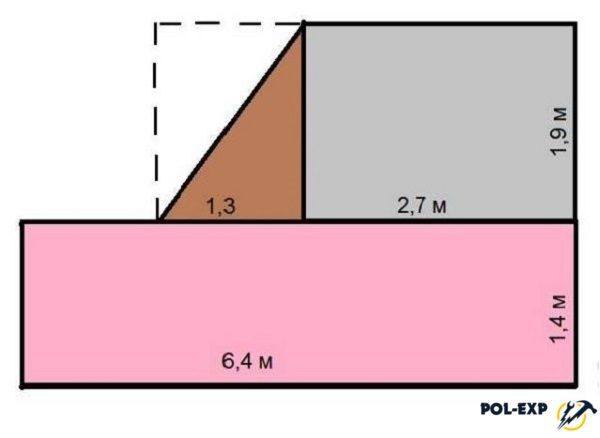
Расчет площади комнаты неправильной формы

Площадь многоуровневых полос посчитать не так сложно, как кажется. Просто считаются площади отдельных сегментов и суммируются. Если ступени необходимо отделать таким же напольным материалом, как и остальной пол, то достаточно измерить площадь боковой части каждой ступени и приплюсовать к общей цифре.

Если комната имеет формулу трапеции, то высчитать ее площадь можно без дележки помещения на простые фигуры. Формула трапеции вычисляется так: длина верхней границы (более короткой стороны – а) суммируется с длиной нижней границы (b), затем умножается на высоту трапеции (h) и полученный результат делится на два. Площадь четырехугольника с равными сторонами рассчитать можно по формуле: S = а (длина длинной стороны) х h (высота четырехугольника).

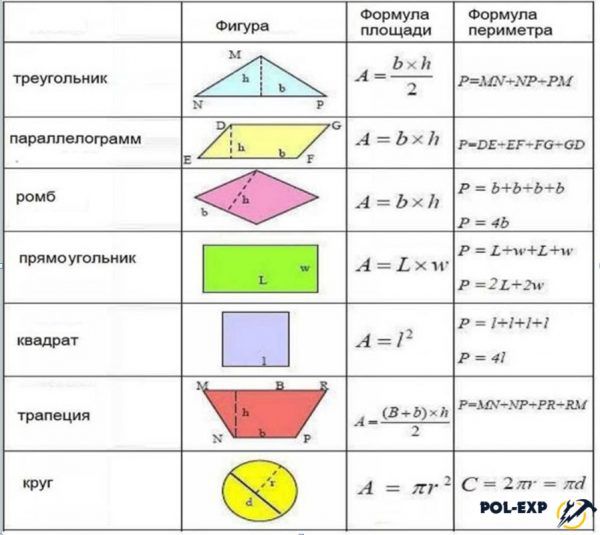
Расчет площадей разных геометрических фигур

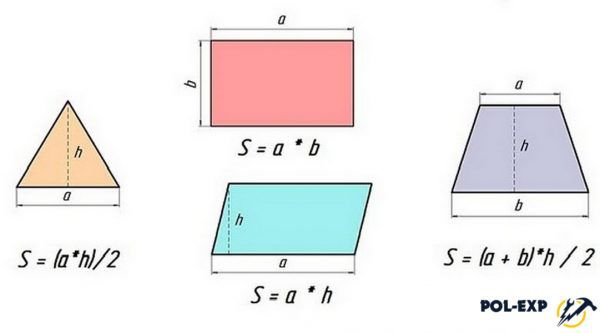
Формулы расчетов

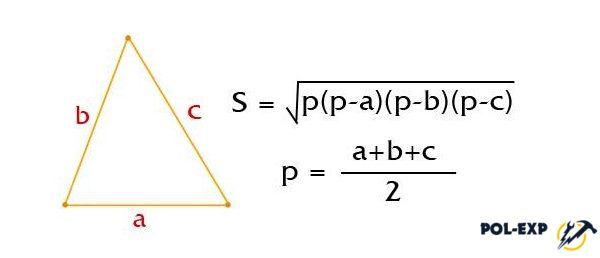
Если треугольник не прямой, то рассчитать его площадь можно с помощью формулы Герона

Пошаговый расчет площади комнаты

Шаг 1. Первым делом необходимо приготовить все измерительные инструменты, а также листок и ручку. На бумаге можно предварительно начертить схему комнаты, стараясь максимально сохранить геометрию и отобразить все ниши и детали помещения. Рулетка используется максимально длинная.

Подготовка всего необходимого

Шаг 2. Измеряется длина комнаты. Если она настолько велика, что рулетки не хватает, то замеры снимаются поэтапно. Для начала производится замер на максимальную длину рулетки, в месте ее окончания делается отметка, от которой потом снова производится замер до конца комнаты.

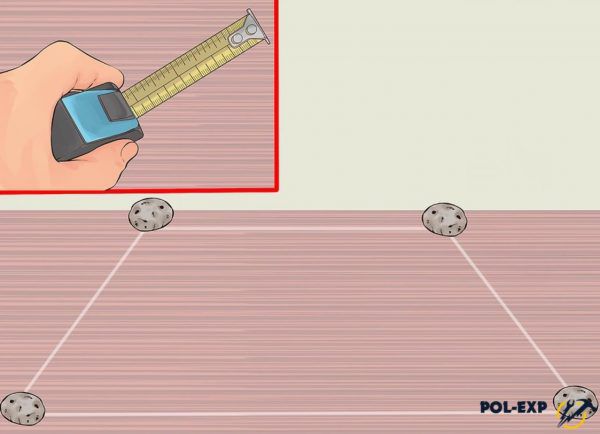
Для начала нужно измерить длину комнаты

Шаг 3. Измеряется ширина комнаты (вдоль стены с меньшей длиной). Рулетка располагается под прямым углом к ранее измеряемой стене комнаты (длине). Полученные данные записываются.

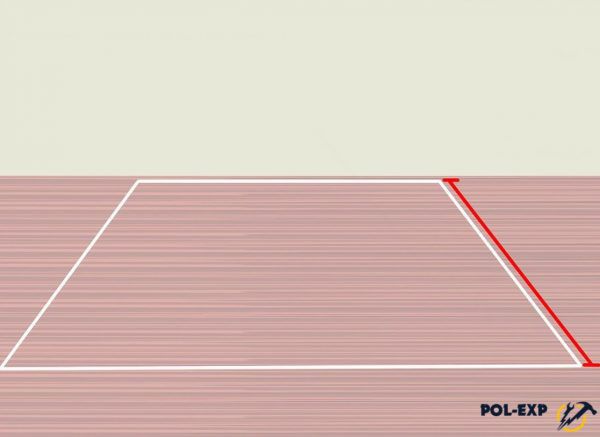
Измеряется ширина комнаты

Шаг 4. Полученные показатели перемножаются между собой. Для этих целей рекомендуется использовать калькулятор. При необходимости значение площади округляется в большую сторону.

Полученная цифра округляется в большую сторону

Шаг 5. Если необходимо измерить площадь сложной геометрически комнаты, то для начала сложная фигура делится на несколько простых – квадратов, треугольников, прямоугольников. Объект изображается на листочке бумаги схематически, схематически делится.

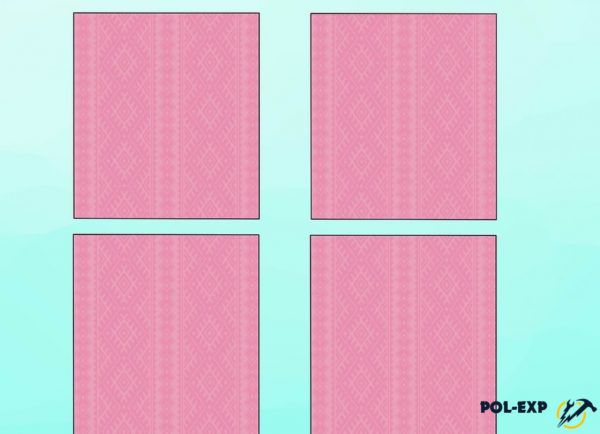
Комната разделена на 4 прямоугольника

Шаг 6. Производится замер каждой фигуры в отдельности. Например, прямоугольники, треугольники.

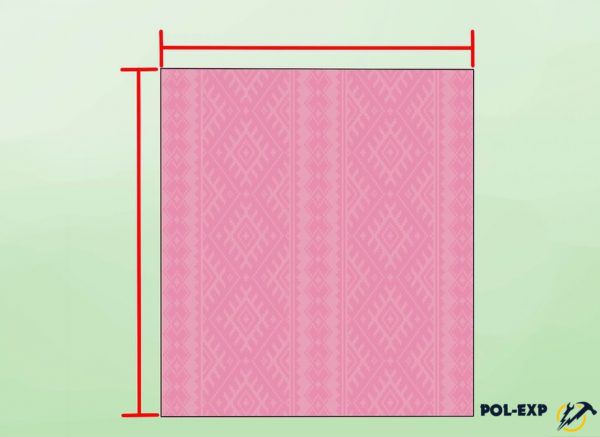
Каждая фигура замеряется отдельно

Шаг 7. Производится вычисление площади каждой фигуры. Далее все полученные значения суммируются и получается полная точная площадь пола комнаты.

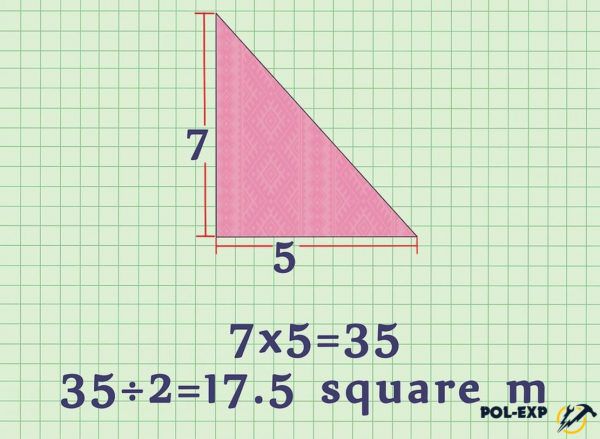
Пример расчета площади треугольника

Инструменты для определения квадратных метров

Для расчета площади стен потребуются:

• Строительный уровень, помогает удостовериться в ровном расположении меток, линий.
• Чтобы правильно вычислить площадь, потребуется рулетка.
• Используя угольник, можно удостовериться в правильности углов.

Проверка угла

• На бумаге карандашом чертят чертеж.
• Для точности подсчета, лучше пользоваться калькулятором.

Рисуем схематическое изображение перегородок в комнатах, наносим на чертеж размеры, измеренные рулеткой. Не забудьте обозначить проемы окон, дверей на внешних стенах.

Недостаток расчетов вручную стен в ванной – легко допустить ошибку, пропустив замер одной из сторон. Либо наоборот, посчитать одну сторону два раза.

Вариант расчета – программа 3Д Редактор. Нужно загрузить из интернета на компьютер. Достаточно вбить в поиск 3Д редактор, система предложит варианты.

В программе необходимо нарисовать схематический рисунок комнаты в квартире, указать размеры стен, выемок, выпуклостей. Выделив необходимые участки, получаем точные расчеты размеров.

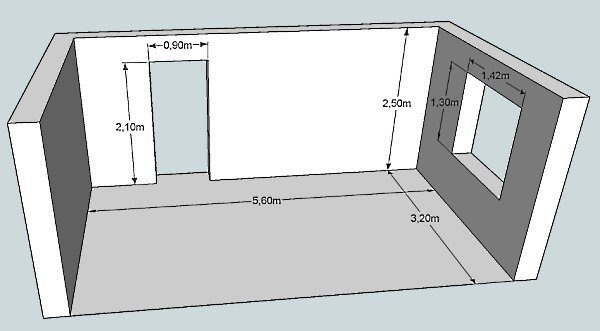
Схематическое изображение на 3Д редакторе

Как узнать площадь окон и дверей?

Площадь, занятая окнами, измеряется по откосам и подоконнику. Высота окна определяется по боковому откосу, ширина – по подоконнику или верхнему откосу.

Например, ширина окна – 1,55 м, высота – 1,65 м.

1,65 х 1,55 = 2,56 м2

Если окон несколько, общая площадь их суммируется.

Площадь треугольного окна: S = 0,5А*h, где А – нижняя сторона/ширина окна, h – высота.

Если ширина треугольного окна 2 метра, а высота – 1,5 метра, то площадь окна составит:

0,5 х 1,5 х 2 = 1,5 м2.

Площадь дверей, также как и площадь прямоугольной стены, измеряется простым умножением ширины двери на высоту. За основу берутся снятые замеры по коробке, а не по полотну.

Прямоугольный треугольник и его площадь.

Прямоугольный треугольник – это треугольник, у которого один угол равен 90 градусам (потому называется прямым). Прямой угол образуют две перпендикулярные линии (в случае с треугольником – два перпендикулярных отрезка). В прямоугольном треугольнике прямой угол может быть только один, т.к. сумма всех углов одного любого треугольника равна 180 градусам. Получается, что 2 других угла должны делить между собой оставшиеся 90 градусов, например 70 и 20, 45 и 45 и т.д. Итак, основное вы вспомнили, осталось узнать, как найти площадь прямоугольного треугольника. Представим, что перед нами вот такой прямоугольный треугольник, и нам необходимо найти его площадь S.

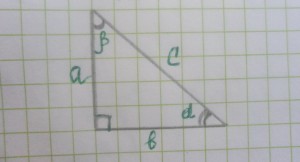
1. Самый простой способ определения площади прямоугольного треугольника высчитывается по следующей формуле:

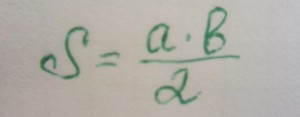
В нашем случае, площадь прямоугольного треугольника равна: S = 2,5 см. * 3 см. / 2 = 3,75 кв.см.

В принципе, больше нет необходимости выверения площади треугольника иными способами, т.к. в быту пригодится и поможет только этот. Но существуют и варианты измерения площади треугольника через острые углы.

2. Для других способов вычисления необходимо иметь таблицу косинусов, синусов и тангенсов. Посудите сами, вот какие варианты вычисления площадей прямоугольного треугольника еще можно использовать:

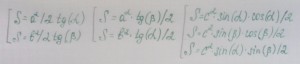
Мы решили воспользоваться первой формулой и с небольшими помарками (чертили в блокноте и использовали старую линейку и транспортир), но у нас вышел верный расчет:

S = (2,5*2,5)/(2*0,9)=(3*3)/(2*1,2). У нас вышли такие результаты 3,6=3,7, но с учетом сдвига клеток, этот нюанс нам можно простить.

Измеряем площадь сложных фигур

Круг и треугольник – сложные фигуры для самостоятельного вычисления. Как измерить квадратные метры окружности, если нет математического или инженерного образования? Опять-таки по формуле.

Как измерить размер окружности

Этап № 1. Замеряем диаметр (это линия, которая проходит через центр круга от одного края окружности к другому). Пускай диаметр будет равняться 3 м. Далее находим радиус – это половина длины диаметра. То есть 1,5 м. Записываем радиус на бумагу.

Этап № 2. Производим расчеты по формуле S = ПR2, где S – это площадь круга, П – постоянное число, а R – радиус окружности. Получается 3,14 x (1,5 x 1,5) = 7, 065. Площадь данного круга – 7,065 кв. м.

Но это площадь целого круга. Арка над дверью – это половина круга. Значит, еще нужно разделить данное число на два и далее прибавить к прямоугольной площади двери. 7,065 : 2 = 3,53 м2.

Как измерить площадь треугольника

Если предыдущий хозяин квартиры был математик, то он вполне мог сделать на потолке треугольные фигуры, которые приходится реставрировать и выделять другим цветом или штукатуркой. Придется считать, чтобы не переплачивать.

Расчет метра квадратного в треугольной фигуре начинается с внимательного осмотра этой фигуры.

Необходимо найти основание треугольника, то есть линию, на которую опираются две других (как крыша на доме). Далее провести линию из противоположной верхушки к основанию. Эти два числа записать.

1. Этап № 1. Разделить основание треугольника на 2 и записать. Это число пригодится в недалеком будущем. Измерить высоту и тоже записать.
2. Этап № 2. Произвести расчет м2 фигуры. Для этого необходимо использовать формулу: S = 0,5аh, где S – площадь треугольника, а – основание, а h – высота. Пример: основание 3 м, высота 2,5 м. Итого: 0,5 x 3 x 2,5 = 3,75. Размер треугольника – 3,75 м2. Записать, чтобы не забыть.

Как найти площадь треугольника

Как вы можете помнить из школьной программы по геометрии, треугольник – это фигура, образованная из трех отрезков, соединяющихся тремя точками, не лежащими на одной прямой. Треугольник образует три угла, отсюда и название фигуры. Определение может быть и иным.

Треугольник можно так же назвать многоугольником с тремя углами, ответ будет так же верным. Треугольники делятся по числу равных сторон и по величине углов в фигурах.

Так выделяют такие треугольники, как равнобедренный, равносторонний и разносторонний, а так же прямоугольный, остроугольный и тупоугольный, соответственно.

Формул вычисления площади треугольника очень много. Выбирать, как найти площадь треугольника, т.е. какой формулой воспользоваться, только вам. Но стоит отметить лишь некоторые обозначения, которые используются во многих формулах вычисления площади треугольника. Итак, запоминайте:

S – это площадь треугольника,

a, b, c – это стороны треугольника,

h – это высота треугольника,

R – это радиус описанной окружности,

p – это полупериметр.

Вот основные обозначения, которые могут вам пригодиться, если вы совершенно забыли курс геометрии. Ниже будут приведены наиболее понятные и не сложные варианты вычисления неизвестной и загадочной площади треугольника. Это не сложно и пригодится как вам в домашних нуждах, так и для помощи своим детям в домашнем задании. Давайте вспомним, как вычислить площадь треугольника проще простого:

В нашем случае площадь треугольника равна: S = ½ * 2,2 см. * 2,5 см. = 2,75 кв.см. Помните, что площадь измеряется в квадратных сантиметрах (кв.см.).

Прямоугольный треугольник и его площадь

Прямоугольный треугольник – это треугольник, у которого один угол равен 90 градусам (потому называется прямым). Прямой угол образуют две перпендикулярные линии (в случае с треугольником – два перпендикулярных отрезка). В прямоугольном треугольнике прямой угол может быть только один, т.к.

сумма всех углов одного любого треугольника равна 180 градусам. Получается, что 2 других угла должны делить между собой оставшиеся 90 градусов, например 70 и 20, 45 и 45 и т.д. Итак, основное вы вспомнили, осталось узнать, как найти площадь прямоугольного треугольника.

Представим, что перед нами вот такой прямоугольный треугольник, и нам необходимо найти его площадь S.

В нашем случае, площадь прямоугольного треугольника равна: S = 2,5 см. * 3 см. / 2 = 3,75 кв.см.

В принципе, больше нет необходимости выверения площади треугольника иными способами, т.к. в быту пригодится и поможет только этот. Но существуют и варианты измерения площади треугольника через острые углы.

2. Для других способов вычисления необходимо иметь таблицу косинусов, синусов и тангенсов. Посудите сами, вот какие варианты вычисления площадей прямоугольного треугольника еще можно использовать:

S = (2,5*2,5)/(2*0,9)=(3*3)/(2*1,2). У нас вышли такие результаты 3,6=3,7, но с учетом сдвига клеток, этот нюанс нам можно простить.

Равнобедренный треугольник и его площадь

Если перед вами стоит задача вычислить формулу равнобедренного треугольника, то проще всего воспользоваться главной и как считается классической формулой площади треугольника.

Но для начала, перед тем, как найти площадь равнобедренного треугольника, узнаем, что это за фигура такая. Равнобедренным треугольником называется треугольник, у которого две стороны имеют одинаковую длину. Эти две стороны называются боковыми, третья сторона называется основанием. Не путайте равнобедренный треугольник с равносторонним, т.е.

правильным треугольником, у которого все три стороны равны. В таком треугольнике нет особых тенденций к углам, точнее к их величине. Однако углы у основания в равнобедренном треугольнике равны, но отличаются от угла между равными сторонами.

Как вы можете заметить, в этих формулах активно используются углы, их величины, косинусы, синусы и тангенсы.

По этой причине, без специальной книжки вам не обойтись, хотя всю информацию вы сможете найти в Интернете.

Отметим только, что в формулах угол альфа – тот, что находится между боковой стороной и основанием, а угол гамма (y) – тот, что находится между равными боковыми сторонами треугольника.

Как посчитать площадь комнаты: методика расчета по полу

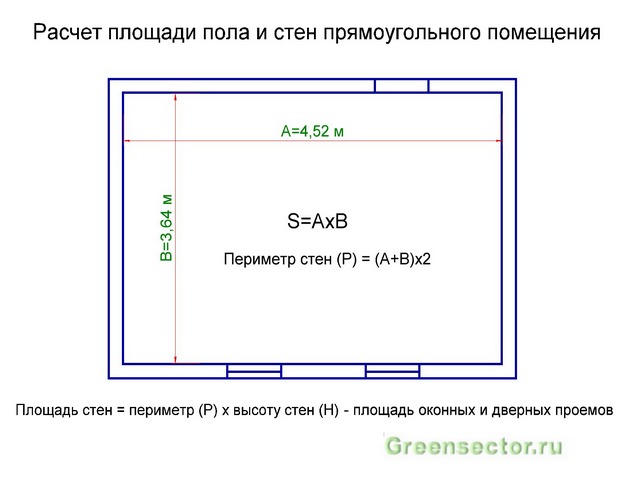
Можно рассчитать площадь пола. Данная процедура состоит из таких этапов. Прежде всего, необходимо освободить стены помещения. Лучше проводить измерения в пустом помещении. Если помещение прямоугольное, то можно перемножить две стороны

В реальности стороны могут немного отличаться, поэтому так важно мерить все стороны. В некоторых случаях комната может быть не правильной конфигурации

В такой ситуации все пространство делится на отдельные прямоугольники. При этом можно нарисовать схему со всеми размерами. Затем считается площадь отдельных участков. Кстати, помещение не обязательно будет состоять только из прямоугольников. Оно может содержать треугольники и даже круги.

Если вы не знаете, как посчитать квадратные метры комнаты, то можно воспользоваться специальным калькулятором. При вычислении габаритов не обязательно соблюдать все размеры до сантиметра. Часто применяется округление значений. Иногда требуется учитывать разные углубления и выступы в стенах.

При расчетах важно учитывать и их предназначение. Если нужно узнать значения для монтажа теплого пола, то можно не учитывать пространство, занятое тяжелой мебелью

Есть варианты, когда в помещении используются разные уровни пола. В подобной ситуации также требуется поделить комнату на отдельные зоны. Не стоит осуществлять замеры по стене, так как она может иметь кривую поверхность.

Сложно определить площадь по полу, имеющего разнообразные выступы в виде волн или полукругов.

Как посчитать площадь комнаты в квадратных метрах

Рассчитать площадь комнаты, часто надо при закупке материалов для строительства или ремонта. Например, некоторые виды напольного покрытия продают на квадраты (то есть, на квадратные метры). Чтобы правильно рассчитать его количество, надо знать площадь пола (часто говорят квадратура комнаты, что по сути одно и то же).

Можно найти площадь комнаты зная длину и ширину

Измерения

Берем рулетку, листок бумаги, карандаш и калькулятор. На бумаге рисуем план комнаты. При помощи рулетки измеряем длины всех стен. Измерения проводим на уровне пола — если постройка старая, велика вероятность того, что стены «завалены» в ту или другую сторону. Тем более что определяем площадь пола, так что логичнее измерять вплотную к стенам, но мерную ленту тянуть по полу.

На схеме проставляем измерения. Лучше всего в метрах. Точность измерений — до сантиметра. Это понадобится при покупке материалов, которые продаются на погонные метры — линолеум, ковролин или другие рулонные покрытия. Чтобы посчитать площадь комнаты в квадратных метрах, тоже желательна такая точность. Хоть можно, конечно, и округлить. Но лучше это сделать уже получив результат.

Как высчитать квадратуру комнаты

Имея длину и ширину комнаты прямоугольной формы, цифры надо просто перемножить. На рисунке выше такая комната нарисована справа. Длинная стена равна 7 м, короткая — 4 метрам. Перемножаем 7*4 = 28 квадратных метров. Это и есть площадь этого помещения, пола. Другими словами, мы нашли квадратуру. Используя эту цифру, можно покупать напольное покрытие. Но надо иметь в виду, что требуется некоторый запас — на подгонку, подрезку. Чем сложнее схема укладки и чем больше фрагменты напольного покрытия, тем запас должен быть больше.

Часто комната не прямоугольная, а имеет более сложную форму. Чтобы посчитать площадь такой комнаты в квадратных метрах, ее разбивают на простые фигуры. Если удается — на прямоугольники или квадраты. Например, Г-образную комнату разбивают на два прямоугольника. Затем считают площадь каждого прямоугольника отдельно, потом их складывают.

Как найти площадь комнаты сложной формы

• Считаем большой прямоугольник: 5 м * 4,35 м = 21,75 м².
• Находим квадратуру маленького: 2,5 м * 2,65 м = 6,625 м².
• Площадь пола в этом помещении равна сумме 21,75 м² + 6,625 м² = 28,375 м².

При покупке материалов, проще пользоваться округленными значениями. Чаще всего говорят, что в этом помещении 28,4 квадрата.

Если помещение имеет участок «срезанной» стены, как на рисунке ниже, проще всего дорисовать прямоугольник так, чтобы косая делила его на два треугольника. В этом случае снова-таки получаем Г-образную комнату. Как высчитать ее площадь уже знаем.

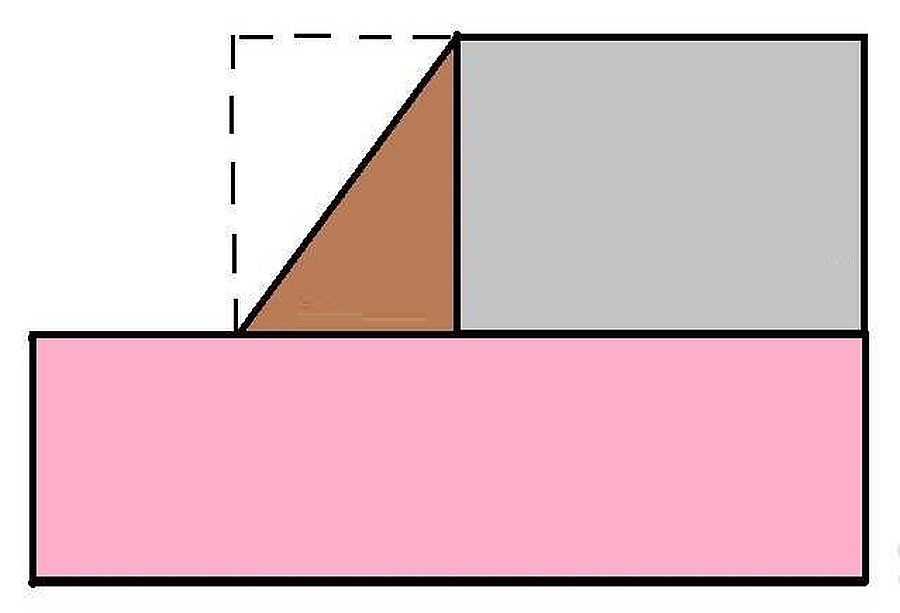Получается, ищем площадь трех прямоугольников

А недостающий участок — это половина маленького прямоугольника. То есть, находим площадь этого маленького прямоугольника, делим ее пополам и прибавляем к размерам Г-образного участка.

Приведем пример расчета подставляя произвольные значения:

• Большой прямоугольник: 1,75 м *1,93 м = 3,3775 м². Для простоты округлим до 3,38 м².
• Средний прямоугольник: 1,18 м * 0,57 м = 0,6726 м². Снова округлим до 0,67 м².
• Самый маленький прямоугольник (в нашем случае это будет квадрат): 0,57 м *0,57 м = 0,3249 м2, после округления имеем 0,33 м².
• Чтобы найти общую площадь складываем квадратуру двух прямоугольников и добавляем половину площади последнего, самого маленького участка. 3,38 + 0,67 +0,33/2 = 3,38 + 0,67 +0,17 = 4,22 м².

Такая методика — разбиение на простые фигуры — самый удобный и простой метод. Всегда стоит стараться преобразовать сложную фигуру в набор простых. Правда, измерений может потребоваться больше.

https://youtube.com/watch?v=YL07nZH5ueY

Как снизить количество отходов

Для решения этого вопроса есть, наверное, единственный способ. Как известно, все полотна выпускаются производителями определенного размера, но есть фирмы, которые выполняют нарезку листов по заданному размеру.

Можно точно отмерив, сделать заказ, который также будет покрыт защитным верхним слоем на местах срезов. В этом случае можно застелить даже 8 метровые полотнища, с вызовов специалиста, который подрежет все на месте.

Такой способ значительно сократит отходы, а также благодаря профессиональным действиям специалистов можно не беспокоиться о понижении эксплуатационных характеристик кровельного покрытия.

К недостатку этого метода можно отнести следующие моменты:

• полотна длиной свыше 5 метров сложнее транспортировать и хранить, в отличие от обычных;
• металлочерепица такой длины также сложна в установке и подъеме;
• стоимость будет немного больше, чем при самостоятельном монтаже, так как за дополнительную услугу придется заплатить.

Расчет площади помещения с несколькими уровнями

Думаете, что таких комнат не бывает? Совершенно напрасно, дом, построенный на склоне, вполне может иметь в планировке уступы, например, так гостиная или кухня может быть поделена на зоны. Впрочем, совершенно не обязательно смотреть на пол, ведь и потолок может состоять из нескольких ярусов в самом обычном типовом помещении. Допустим, вам нужно купить краску для его окраски. Разумеется, в целом площади потолка и пола равны, но вот в местах перепада высот вертикальные откосы тоже имеют некоторую квадратуру. И даже с учетом 10 % запаса к закупаемым материалам их может не хватить. Поэтому считаем.

Если уровни у вас простой формы, с прямоугольными элементами, никаких сложностей не возникнет. Достаточно измерить линейкой высоту вертикальных участков, найти их длину и, использовав формулу S = a . b, определить площадь, с которой суммируется квадратура горизонтальных поверхностей. Если край уступа нависает над более низкой площадкой в виде карниза, суммировать результаты измерений каждого яруса недостаточно, поскольку получится, что не учтена нижняя сторона нависающей части. Для настилания паркета или облицовки плиткой эти места особой роли играть не будут, а вот при окраске могут остаться «белые пятна». Так что при подобном положении дел следует обмерить линеечкой и скрытые участки.

Обмеры рулеткой или иным приспособлением лучше выполнять ближе к основанию, поскольку стены могут иметь небольшую кривизну, что даст определенную погрешность в результате.

Сложнее всего выполнять расчет площади помещения при наличии уступов округлой или более сложной формы. В этом случае нужно точно измерить каждую дугу по краю, либо короткими отрезками, либо сразу целиком посредством рулетки и воспользовавшись чьей-нибудь помощью. Затем, найдя радиусы и раздробив поверхности на отдельные геометрические фигуры, используем приведенные выше формулы и находим площадь каждого уступа. Что касается вертикальных участков, о них также было сказано выше, разницы между прямым вариантом и изогнутым нет никакой, если известен периметр.

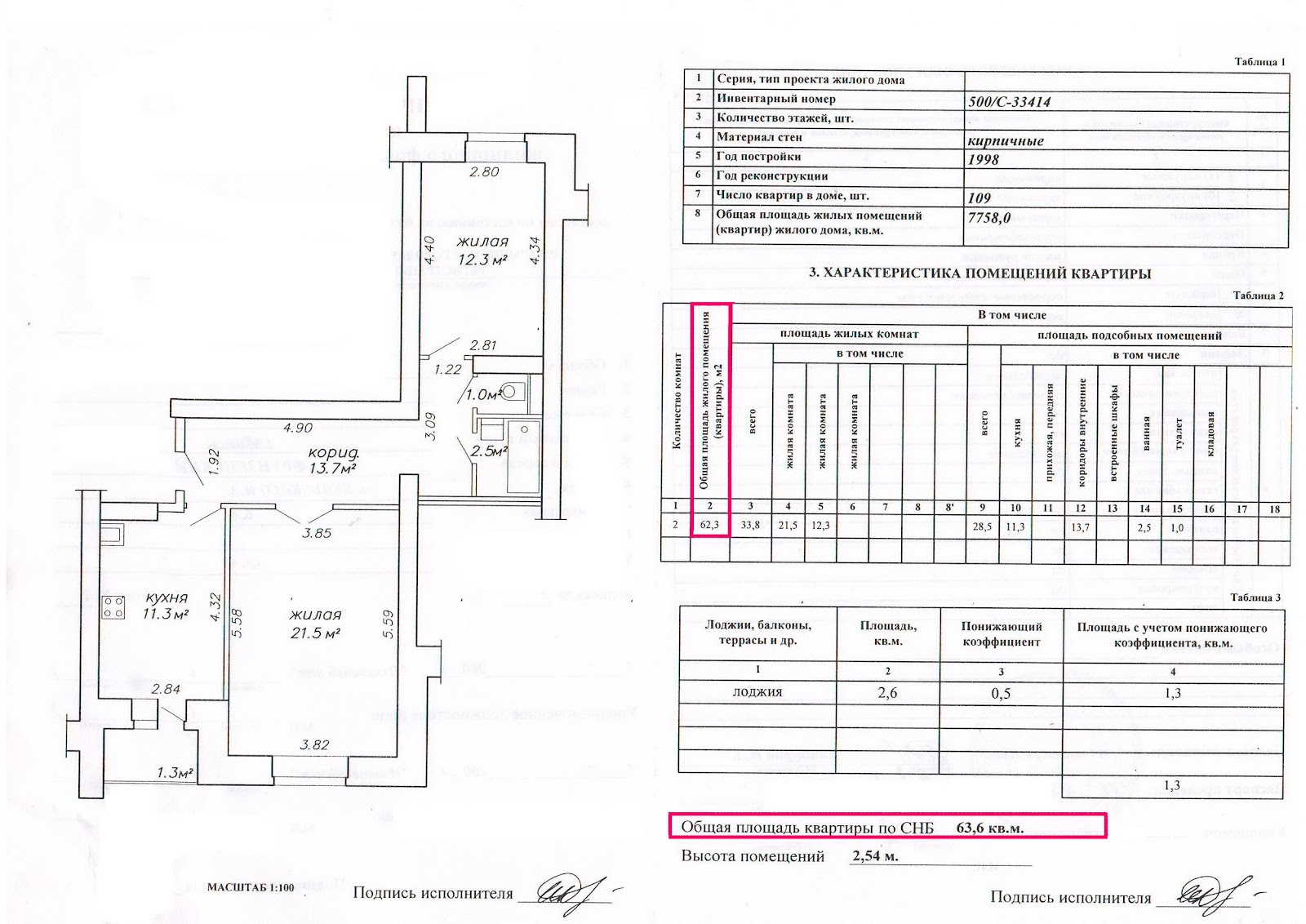
Определение общей и жилой площади квартиры.

Для того чтобы узнать общую и жилую площади квартиры, понадобится снять размеры у всех помещений, включая лоджии, кладовки, встроенные шкафы и т.д.

В документах, получаемых вместе с ордерами и ключами на квартиру, должна быть отражена вся информация о жилой и нежилой площади, но на практике приходится часто проводить повторные расчеты.

Итак, как рассчитать жилую площадь квартиры? Для этого поэтапно измеряются площади всех жилых комнат. Жилой комнатой или жилым помещением считается помещение, пригодное для постоянного места проживания, отвечающее санитарно-техническим правилам и нормам. Это гостиная, спальня, детская. Нежилые комнаты – это коридоры, кладовки, кухня, санузлы.

Знать размеры и площадь всех нежилых помещений необходимо для определения общей площади квартиры. Есть еще понятие отапливаемой и неотапливаемой площади квартиры. Оно также тесно связано со значением «общая», так как рассчитать общую площадь квартиры согласно правилам можно, зная этот метраж.

Общая площадь включает в себя площадь всех жилых и всех неотапливаемых помещений: балконов, лоджий, холодных кладовых, встроенных гардеробных или шкафов. Для включения в общую площадь веранд, лоджий и балконов применяются понижающие коэффициенты. Для лоджий – 0,5; веранд и кладовых – 1,0; для балконов и террас – 0,3.

Грамотно проведенные расчеты помогут подготовиться к любому ремонту, оптимизировать затраты на приобретение материалов, а также проконтролировать расходы на оплату мастерам-отделочникам.

Вычисление площади треугольника по трем сторонам. Формула Герона

Можно долго описывать свойства биссектрисы или медианы треугольника, однако, у нас другая задача: можно ли, зная длины всех сторон ∆АВС, найти его площадь? Такая необходимость возникает, если мы измерили три стороны треугольника, а углы нам неизвестны. Конечно, можно. Уже в I веке нашей эры была известна замечательная формула, позволяющая без проблем находить площади любых треугольников только по трем сторонам.

Эта формула, ныне известная как формула Герона (по имени древнегреческого ученого Герона Александрийского, жившего в I веке н. э., в чьей книге под названием «Метрика» эту формулу и обнаружили), была открыта знаменитым Архимедом. Она очень проста и сводится к следующему:

Как получить формулу Герона?

Как же была получена столь замечательная формула? Все очень просто. Если вы запасетесь небольшим терпением, то сами сможете убедиться, как же легко можно прийти к формуле Герона. Для этого поднимите из памяти на свет вашего разума известные со школьной скамьи теоремы синусов и косинусов. Как они звучат?

Используя их, вы сами придете к желаемому результату, как это сделал много веков назад знаменитый математик. Вот вам небольшая подсказка: используйте формулу площади ∆ABC подвум сторонам и углу между ними. Удачи!

Вариации формулы Герона

Существуют и другие формы записи этой формулы. Вот они:

• S=¼•√((a²+b²+c²)²-2 (a⁴+b⁴+c⁴));
• S=¼•√(2 (a²b²+a²c²+b²c²)-(a⁴+b⁴+c⁴));
• S=¼•√((a+b-c)(a-b+c)(-a+b+c)(a+b+c));
• S=¼•√(4a²b²-(a²+b²-c²)²).

Еще формулы для вычисления площади треугольника:

• S=½•ab•sin γ, где γ — угол между ст-нами a и b;
• S=½•a²/(ctg β+ctg γ), где β и γ — углы, прилежащие к ст-не а;
• S=½•ah, где h — высота, опущенная на ст-ну а;
• S=½•ab, если ∆ABC — прямоугольный;
• S=¼•a²√3, если ∆ABC — равносторонний со ст-ной а;
• S=½•а²•sin φ, если ∆ABC — равнобедренный с боковыми ст-нами, а и углом φ между ними.

Примеры

Эти примеры помогут вам лучше освоить тему:

Пример №1

Вычислить площадь ∆АВС, если a=10, в=20, c=30. Решение. Находим полупериметр: p=(10+20+30)/2=30. Теперь по формуле Герона: S=√(30•(30−10)•(30−20)•(30−30))=0, т. е. на самом деле мы имеем дело не с треугольником, а с отрезком, у которого с=а+b=10+20=30.

Пусть а=3, в=5, c=6, тогда p=(3+5+6)/2=7. Искомая площадь S=√(7•(7−3)•(7−5)•(7−6))=√(7•4•2•1)=√56≈7,48.

Пример №2

Найти угол γ между сторонами треугольника a и в из предыдущей задачи. Решение. S=(aв/2)•sin γ, sin γ=2S/(aв)=2•√56/(3•5)=0,99778, γ=arcsin 0,99778≈86°.

Пример №3

Пусть даны координаты вершин ∆ABC: А (1,2), В (-1,3), С (2,-5). Найти его площадь по одной из формул. Решение. Находим длины его сторон: AB=√((-1−1)²+(3−2)²)=√5, BC=√((2-(-1))²+(-5−3)²)=√73, AC=√((2−1)²+(-5−2)²)=√50. Тогда S=¼•√(4•5•73-(5+73−50)²)=¼•√676=26/4=6,5.

Пример №4

Периметр равностороннего треугольника численно равен его площади. Чему равна его сторона а? Решение. Так как периметр равностороннего треугольника равен Р=3а, а его площадь S=¼•a²√3, то приравняв эти равенства, получим: 3а=¼•а²√3. Решив это уравнение, найдем: а=4√3.

Пример №5

Площадь круга радиусом R равна площади равностороннего ∆ABC. Найти радиус круга. Решение. Площадь круга S=πR² по условию задачи равна площади равностороннего ∆ABC: πR²=¼•а²√3. Из этого соотношения находим: R=а√(√3)/(2√π)≈0,3713а.

Пример №6

Сторона и два прилежащих к ней угла в ∆ABC равны соответственно а=7, β=30°, γ=60°. Чему равна его площадь? Решение. S=½•7²/(ctg 30°+ctg 60°)=(49/2)/(√3+1/√3)=49√3/8≈10,61.

Калькулятор площади пола

Чтобы не мучиться с ручными расчетами на бумаге и не осваивать компьютерные программы, можно воспользоваться помощью онлайн-калькуляторов. Такую возможность предоставляет масса Интернет-ресурсов. В специальном окошке достаточно ввести все данные, и после нажатия кнопки «рассчитать» в новом поле или на новой странице откроются итоговые посчитанные данные. Обычно все показатели вводятся в метрах, но по желанию можно указать и другие единицы измерения.

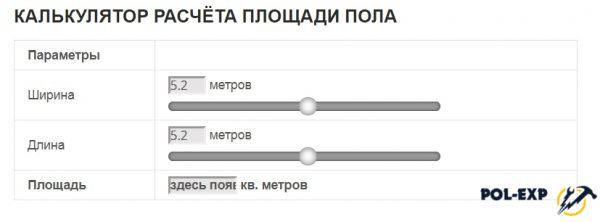
У онлайн-калькуляторов есть свои плюсы и минусы

Достоинства онлайн калькуляторов:

• не нужно считать вручную;
• можно легко получить площадь любой фигуры;
• скорость расчетов и их точность высоки.

Треугольники.

Как вы можете помнить из школьной программы по геометрии, треугольник – это фигура, образованная из трех отрезков, соединяющихся тремя точками, не лежащими на одной прямой. Треугольник образует три угла, отсюда и название фигуры. Определение может быть и иным. Треугольник можно так же назвать многоугольником с тремя углами, ответ будет так же верным. Треугольники делятся по числу равных сторон и по величине углов в фигурах. Так выделяют такие треугольники, как равнобедренный, равносторонний и разносторонний, а так же прямоугольный, остроугольный и тупоугольный, соответственно.

Формул вычисления площади треугольника очень много. Выбирать, как найти площадь треугольника, т.е. какой формулой воспользоваться, только вам. Но стоит отметить лишь некоторые обозначения, которые используются во многих формулах вычисления площади треугольника. Итак, запоминайте:

S – это площадь треугольника,

a, b, c – это стороны треугольника,

h – это высота треугольника,

R – это радиус описанной окружности,

p – это полупериметр.

Вот основные обозначения, которые могут вам пригодиться, если вы совершенно забыли курс геометрии. Ниже будут приведены наиболее понятные и не сложные варианты вычисления неизвестной и загадочной площади треугольника. Это не сложно и пригодится как вам в домашних нуждах, так и для помощи своим детям в домашнем задании. Давайте вспомним, как вычислить площадь треугольника проще простого:

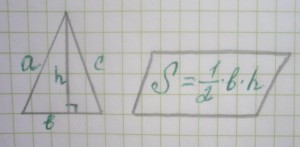
В нашем случае площадь треугольника равна: S = ½ * 2,2 см. * 2,5 см. = 2,75 кв.см. Помните, что площадь измеряется в квадратных сантиметрах (кв.см.).

Прямоугольные помещения

Если комната имеет правильную (относительно) прямоугольную форму, без всевозможных выступов или ниш, то площадь ее вычисляется довольно просто. Для начала, нужно измерить длину и ширину комнаты, после чего результаты записать на бумажке, чтобы не забыть. Измерения можно производить как в метрах, так и в сантиметрах. Если замеры осуществляются в метрах, то после целых значений метров ставится запятая, а потом пишутся сантиметры. Например, 4 метра, 35 сантиметров следует записать: 4,35 м.

Измерив длину, например, 2,35 м и ширину 1,4 м, данные перемножаются. Например: 2,35 м х 1,4 м. В результате получается 3,290 м2 или 3,29 м2. Как правило, после запятой всегда оставляется две цифры. Если их больше, то значение округляется по правилам, которые излагались еще в начальных классах школы. При этом, можно округлять или до метров, или до сантиметров, в зависимости от требуемой точности. В основном, достаточно измерять с точностью до метров и лишь изредка требуется точность до сантиметров.

Общие рекомендации

Для получения точных цифр строители рекомендуют измерять стену в трёх местах (в начале, середине и в конце). После чего полученные данные стоит суммировать и разделить на 3 и таким образом высчитать среднее арифметическое. Подобная процедура помогает избежать погрешности, даже если стены не самые ровные.

При измерении оконных и дверных проёмов не стоит рассчитывать правильность их формы.

Измерение проёма окна

Лучше собственноручно перемерить все четыре стороны, а не только две соприкасающиеся. Такой подход обезопасит вас от последствий халатности строителей и лишних затрат (например, при замене окон или дверей).

Каковой бы не была причина, по которой вы всё же решили выяснить, как самостоятельно посчитать площадь помещения — помните, что любую работу желательно делать качественно. Поэтому постарайтесь тщательно спланировать весь процесс, подготовьте необходимые инструменты, и смело приступайте к проведению замеров и вычислениям. А наши советы, надеемся, смогут облегчить вам их выполнение.

Доборные элементы

Расчет дополнительной фурнитуры

Для полноценного монтажа необходима дополнительная фурнитура, так называемые доборные элементы. Такие детали можно приобрести как дополнительно, так и в комплекте с металлочерепицей. В первую очередь они необходимы для надежности кровли, в особенно ненадежных местах, а уже потом их можно рассматривать как часть декорации.

Элемент можно купить в среднем – 200 рублей за погонный метр. Но нужно подумать, что нам необходимо и для чего, а также подсчитать, во сколько это обойдется, в случае если придется покупать.

Итак, рассмотрим, нам необходимо:

1. Конек, планки торцевые, которые будут защищать от атмосферных явлений – дождь, ветер, и планка примыкания – для дополнительной герметизации различных стыков, к примеру, печной трубы. И это только самое необходимое, есть еще другие дополнительные детали, и они особенно необходимы, если система кровли сложная, многоскатная.
2. Барьер снеговой – для защиты водостока от внезапного обрушения снега, карнизная планка – защищает от попадания под конек пыли и грязи. Мы сейчас рассмотрим, как подсчитать самые необходимые комплектующие элементы, а потом исходя из расчетов, вы окончательно решите, что приобретать. Чтобы подсчитать количество фурнитуры нужно:
   • измерить длину конька, все будет зависеть, каких размеров будут планки, так как на стыки уходит 10 см, стандартный конек – 2 метра, к примеру, если длина конька 6 м, то понадобится покупать 4 планки, а это 800 рублей;
3. торцевые планки выпускаются разной длины, так и монтируются на торцевых скатах, высчитывается аналогичным образом, то есть с учетом, что на стыки должно уходить 10 см;
4. планка примыкания – рассчитывается по описанному выше принципу.

Кроме этого, необходимы саморезы стоимость их варьируется от 3 до 7 рублей за штуку. После подсчетов, можно подумать о цвете, если вы хотите, чтобы ваш дом выделялся и был виден издалека, то выбирайте любой яркий цвет. Качественно выполненная черепица не выгорает на солнце и не теряет своих качеств, и вы можете не беспокоиться, что со временем ваша крыша потеряет свой первоначальный вид.

Формулы

Первый способ. Чтобы найти площадь треугольника, надо найти полупроизведение двух его сторон на синус угла между ними (рис. 1).
То есть если известны длины двух сторон треугольника
$ABC$, которые равны
$a$ и
$b$, а также угол
$\alpha$ между этими сторонами, то искомая площадь:

Второй способ. Чтобы найти площадь треугольника, нужно сторону умножить на высоту, проведенную к этой стороне (рис. 2),
и полученное произведение поделить на два. То есть если сторона треугольника
$ABC$ равна
$a$, а длина высоты, проведенной к этой стороне
— $h_{a}$, то имеет место формула:

Третий способ. Чтобы найти площадь треугольника
$ABC$, если известны длины всех его трех сторон
$a$,
$b$ и
$c$, нужно воспользоваться формулой Герона:

где $p=\frac{a+b+c}{2}$ — полупериметр.

Четвертый способ. Чтобы найти площадь треугольника
$ABC$, нужно радиус
$r$ вписанной в этот треугольник окружности умножить на полупериметр
$p$ треугольника:

Пятый способ. Чтобы найти площадь треугольника со сторонами
$a$,
$b$ и
$c$, нужно произведение этих сторон поделить на четыре радиуса
$R$, описанной около треугольника окружности: