Правило золотого сечения в архитектуре, строительстве и дизайне

Математические свойства

• Φ{\displaystyle \Phi } — иррациональное алгебраическое число, положительное решение квадратного уравнения x2−x−1={\displaystyle x^{2}-x-1=0}, откуда, в частности, следуют соотношения:

  Φ2−Φ=1,{\displaystyle \Phi ^{2}-\Phi =1,}

  Φ⋅(Φ−1)=1.{\displaystyle \Phi \cdot (\Phi -1)=1.}

• Φ{\displaystyle \Phi } — представляется через тригонометрические функции:
  • Φ=2cos⁡π5=2cos⁡36∘.{\displaystyle \Phi =2\cos {\frac {\pi }{5}}=2\cos 36^{\circ }.}
  • Φ=2sin⁡(3π10)=2sin⁡54∘.{\displaystyle \Phi =2\sin(3\pi /10)=2\sin 54^{\circ }.}

1Φ=φ=tg⁡(arctg⁡(2)2)=21+1+22=21+5=5−12.{\displaystyle {\frac {1}{\Phi }}=\varphi =\operatorname {tg} \left({\frac {\operatorname {arctg} (2)}{2}}\right)={\frac {2}{1+{\sqrt {1+2^{2}}}}}={\frac {2}{1+{\sqrt {5}}}}={\frac {{\sqrt {5}}-1}{2}}.}

• Φ{\displaystyle \Phi } представляется в виде бесконечной цепочки квадратных корней:

  Φ=1+1+1+1+….{\displaystyle \Phi ={\sqrt {1+{\sqrt {1+{\sqrt {1+{\sqrt {1+\dots }}}}}}}}.}

• Φ{\displaystyle \Phi \;} представляется в виде бесконечной цепной дроби

  Φ=1+11+11+11+…,{\displaystyle \Phi =1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\dots }}}}}},}

подходящими дробями которой служат отношения последовательных чисел Фибоначчи Fn+1Fn{\displaystyle {\frac {F_{n+1}}{F_{n}}}}. Таким образом,

• Φ=limn→∞Fn+1Fn.{\displaystyle \Phi =\lim _{n\to \infty }{\frac {F_{n+1}}{F_{n}}}.}

• Мера иррациональности Φ{\displaystyle \Phi } равна 2.

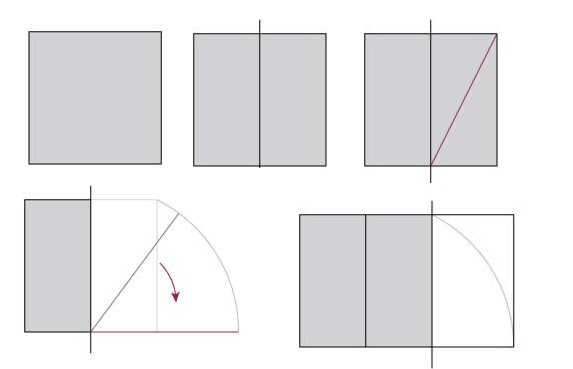
Отрезание квадрата от прямоугольника, построенного по принципу золотого сечения

Отрезав квадрат от прямоугольника, построенного по принципу золотого сечения, мы получаем новый, уменьшенный прямоугольник с тем же отношением сторон Φ=a/b{\displaystyle \Phi =a/b}, что и у исходного прямоугольника Φ=(a+b)/a{\displaystyle \Phi =(a+b)/a}.

Золотое сечение в пятиконечной звезде

В правильной пятиконечной звезде каждый отрезок делится пересекающим его отрезком в золотом сечении. На приведённом рисунке отношения красного отрезка к зелёному, зелёного к синему и синего к пурпурному равны Φ{\displaystyle \Phi }. Кроме того, отношение красного отрезка к расстоянию между соседними вершинами звезды, которое равно зелёному отрезку, также равно Φ{\displaystyle \Phi }.

Построение золотого сечения

Геометрическое построение. Золотое сечение отрезка AB{\displaystyle AB} можно построить следующим образом: в точке B{\displaystyle B} восстанавливают перпендикуляр к AB{\displaystyle AB}, откладывают на нём отрезок BC{\displaystyle BC}, равный половине AB{\displaystyle AB}, на отрезке AC{\displaystyle AC} откладывают отрезок CD{\displaystyle CD}, равный BC{\displaystyle BC}, и наконец, на отрезке AB{\displaystyle AB} откладывают отрезок AE{\displaystyle AE}, равный AD{\displaystyle AD}. Тогда

Φ=|AB||AE|=|AE||BE|.{\displaystyle \Phi ={\frac {|AB|}{|AE|}}={\frac {|AE|}{|BE|}}.}

Другой способ построить отрезок, равный по длине числу золотого сечения

Другой способ построить отрезок, равный по длине числу золотого сечения, — начертить сначала квадрат ABCD со стороной 1. После этого одну из сторон, например сторону AD, разделить точкой E пополам, так что AE=DE=1/2. От точки B или C до точки E провести гипотенузу треугольника АВЕ или DCE. Согласно теореме Пифагора ВE=СE=52{\displaystyle {\frac {\sqrt {5}}{2}}}. Затем провести дугу с центром в точке Е от точки В или точки С до момента её пересечения с продолжением стороны АD (точкой пересечения дуги и продолжения стороны АD пусть будет точка Н). Как радиусы круга BE=СЕ=ЕН. Так как АН=АЕ+ЕН, результатом будет отрезок АН длиной Φ{\displaystyle \Phi }. Так как DH=EH-ED, другим результатом будет отрезок DH длиной φ{\displaystyle \varphi }.

• Отношение диагонали правильного пятиугольника к стороне равно золотому сечению.
• Значения дроби после запятой для Φ{\displaystyle \Phi }, 1Φ{\displaystyle {\frac {1}{\Phi }}} и Φ2{\displaystyle \Phi ^{2}} в любой системе счисления будут равны.
• ∑n=1∞(−1)n+1n2(2nn)=2ln2⁡φ{\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n^{2}{\binom {2n}{n}}}}=2\ln ^{2}\varphi }

Тогда как ∑n=1∞1n2(2nn)=π218{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}{\binom {2n}{n}}}}={\frac {\pi ^{2}}{18}}}[источник не указан 1010 дней]

Золотое Сечение в действии

Считается, что Золотое Сечение используется уже около 4000 лет в искусстве и дизайне. Однако, многие люди соглашаются, что при строительстве Египетских Пирамид также использовался этот принцип.

В более современные времена это правило может быть замечено в музыке, искусстве и дизайне вокруг нас. Применяя аналогичную рабочую методологию, вы можете привнести в свою работу те же особенности дизайна. Давайте взглянем на несколько вдохновляющих примеров.

Греческая архитектура

В древнегреческой архитектуре Золотое Сечение использовалось для определения приятных пространственных отношений между шириной здания и его высотой, размером портика и даже положением колонн, поддерживающих структуру.

В результате получается идеально пропорциональное строение. Движение неоклассической архитектуры также использовало эти принципы.

Тайная вечеря

Леонардо Да Винчи, как и многие другие художники прошлых лет, часто использовал Золотое Сечение для создания приятных композиций.

В Тайной вечере фигуры расположены в нижних двух третях (самая большая из двух частей Золотого Сечения), а Иисус идеально зарисован между золотых прямоугольников.

Золотое сечение в природе

Существует множество примеров Золотого Сечения в природе – их вы можете обнаружить вокруг себя. Цветы, морские раковины, ананасы и даже пчелиные соты демонстрируют одинаковое соотношение.

Идеальный треугольник и пентаграмма

Идеальным называют равнобедренный треугольник, основание которого относится к длине стороны как 1/3. То есть, снова-таки соблюдается золотое сечение. Начертить треугольник с идеальным соотношением сторон несложно. Удобнее циркулем, но можно обойтись и линейкой.

Золотой треугольник, правило его построения и применение в создании интерьера, например

Построение такое. На прямой от точки A трижды откладываем отрезок произвольной длины. Эту длину обозначим O. Получаем точку B. Через нее проводим прямую, перпендикулярную отрезку AB. На этой линии в обе стороны от точки B откладываем величину O. Получаем две точки d и d1. Соединяем их с точкой A. Вот и получили треугольник, стороны которого относятся как 1,62. Проверить это можно, если отложить при помощи циркуля длину основания на боковой стороне (точка C). Вторая проверка — противолежащий угол составляет 36°.

Построение пентаграммы несколько сложнее. Ее вписываем в круг, без циркуля не обойтись.

• Центр окружности обозначаем O, через него проводим прямую до пересечения с окружностью. Одну из точек пересечения обозначаем A. Отрезок OA — диаметр окружности.
• Находим середину отрезка OD, ставим точку E. Из центра окружности вверх до пересечения с окружностью восстанавливаем перпендикуляр. Это точка D.

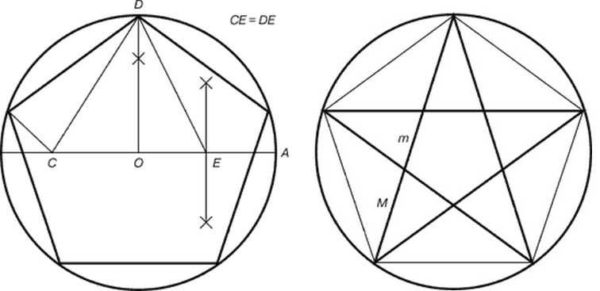
Построение пентаграммы

• Соединяем точки E и D. При помощи циркуля откладываем на радиусе точку C. Отрезок СD равен длине отрезка ED. Циркулем замеряем длину отрезка ED. Иглу ставим в точку E, ведем грифель до пересечения с радиусом. Вот и получили точку C.
• Длинна отрезка DC — сторона пентаграммы. Замеряем ее, при помощи циркуля переносим на окружность. Для этого циркулем с отложенным расстоянием ставим еще четыре точки на окружности, поочередно соединив их, получаем пентаграмму.

Вот что интересно, если вершины полученной пентаграммы использовать для прорисовки звезды, она будет состоять из идеальных треугольников.

https://youtube.com/watch?v=c3SVIQBXMnA

Построение кадра

Для того чтобы грамотно выстроить композицию будущей фотографии, можно воспользоваться обсуждаемым правилом. Эта система композиции представляет собой адаптированный для фотографии и упрощенный вариант золотого сечения, на котором базируется структура всех живых объектов. Этот закон, используемый в фотографии, выглядит следующим образом. Он позволяет определить и установить зрительные центры поля изображения. Иногда они могут называться точками силы или зонами притяжения. Всё поле зрения или кадр, который видит фотограф через видоискатель, следует разделить на девять частей, проведя две горизонтальных и две вертикальных линии.

Точки, образующие центральный прямоугольник стоят от границ кадра на 3/8 и 5/8

Именно на том, что располагается в этих четырёх точках, акцентируется внимание наблюдателя. Несколько меньшее значение придаётся самим прямым линиям, но и они играют в правиле третей важную роль. Поскольку правило третей в фотографии не обязательно должно соответствовать идеальному золотому сечению, то в упрощенном варианте, кадр делится на три равные части вдоль каждой из сторон

У большинства моделей фотоаппаратов такая сетка уже имеется в поле видоискателя. Некоторые модели позволяют включать или отключать сетку по необходимости. Для усиления эффекта восприятия и акцентирования внимания на определённые детали изображения, в фотографии могут использоваться следующие приёмы:

Поскольку правило третей в фотографии не обязательно должно соответствовать идеальному золотому сечению, то в упрощенном варианте, кадр делится на три равные части вдоль каждой из сторон. У большинства моделей фотоаппаратов такая сетка уже имеется в поле видоискателя. Некоторые модели позволяют включать или отключать сетку по необходимости. Для усиления эффекта восприятия и акцентирования внимания на определённые детали изображения, в фотографии могут использоваться следующие приёмы:

• Правило третей;
• Золотое сечение;
• Принцип диагоналей;
• Линия Хогарта;
• Спираль Карню.

В основе всех этих правил лежат попытки привести творческий процесс художника и его видение окружающего мира, к математическому моделированию. Но далеко не всегда поставленная цель может быть достигнута математическими методами.

Как использовать золотое сечение в жизни.

В этой статье речь пойдет об очень важном секрете, о котором знают немногие бизнесмены, и незнание которого часто приводит к развалу бизнеса. Есть такие известные понятия, как «золотое сечение» и «числа Фибоначчи».Ряд Фибоначчи – это когда сумма двух предыдущих чисел дает следующее число

Т.е. 0,1,1,2,3,5… и т.д. В природе все построено по этому принципу. Например, если подсчитать веточки дерева, можно убедиться, что с увеличением радиуса кроны их число увеличивается по закону золотого сечения.Прямоугольник с отношением сторон 0.618 и 0.382 — золотой прямоугольник. Если от него отрезать квадрат, то останется вновь золотой прямоугольник. Этот процесс можно продолжать до бесконечности.Другой всем знакомый пример — пятиконечная звезда (она же магический символ, пентаграмма), в которой каждая из пяти линий делит другую в точке золотого сечения, а концы звезды являются золотыми треугольниками.Скелет человека также построен по этому закону. Он выдержан в пропорции, близкой к золотому сечению. И чем ближе пропорции к формуле золотого сечения, тем более идеальным выглядит внешность человека. Если расстояние между ступней человека и точкой пупа = 1, то рост человека = 1.618 (разумеется, это в идеале). Число 1.618 и есть коэффициент золотого сечения.Но какое отношение это имеет к бизнесу, деньгам, финансам?! Так вот, самое непосредственное! Закон Фибоначчи и есть та самая формула, по которой добывают богатство во все времена. И все, что вы будете предпринимать в соотношении с числами золотого сечения, будет обречено на успех. И наоборот, игнорирование этого правила приводит к краху. Это своего рода магия денег.Рассмотрим применение закона золотого сечения в бизнесе на практике. Допустим, вы купили ящик апельсинов за 1 доллар (доллар в данном случае условная единица) и продали за 2 доллара. Получили прибыль 100%. Как действовать дальше? Купить на эти 2 доллара еще 2 ящика и продать?НЕТ! Вот это и есть самая распространенная ошибка горе-бизнесменов! Правильно будет, в соответствии с законом золотого сечения, купить еще один ящик, продать с теми же 100% прибыли, и только потом купить 2 ящика. То есть действуем по указанному принципу:0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181,6765,10946,17711,28657,46368,75025,121393,196418,317811, Как видим, всего за 32 цикла мы достигли прибыли свыше миллиона! И при этом у нас еще и всегда оставались «лишние» деньги! Кроме того, этот принцип — хорошая страховка от форс-мажорных обстоятельств. Ведь если в самом начале, получив прибыль в 1 доллар и имея 2 доллара на руках и вложив их все сразу, есть риск потерять все. А так у нас доллар в запасе остался, во всяком случае, не в минус уйдем.Особенно важна эта схема при игре на бирже и прочих сравнительно рискованных финансовых операциях. Пример схематичный, его можно адаптировать к прибыли и в 20%, и к любой другой. Используйте в своих расчетах число 1,618 – коэффициент, по которому следует увеличивать финансы, и вам будет сопутствовать успех!Любую деятельность разумно соотносить с принципом золотого сечения. Это самый надежный и безопасный путь. Главное, определиться с единицей измерения. Это может быть время, этапы в работе и т.д. и т.п. Обогащайтесь также поэтапно, согласуя свои шаги с законами природы.

Золотое сечение, как построить. Просто о сложном: что это такое – правило золотого сечения

Золотое сечение –это правило общей пропорции, которая создает универсальную композицию. Математики называют её формулой божественной гармонии или асимметричной симметрией.

Это интересно!  Общее определение правила ЗС –меньшая величина относится к большей, как большая к целому. Было рассчитано приблизительное число, равное 1,6180339887, это и есть коэффициент золотого сечения. Если смотреть в процентном соотношении, то в одном целом меньшая величина занимает 38%, большая – 62%.

Признано считать, что ЗС пришло к нам еще с древней Греции, но есть и такое мнение, что его греки подсмотрели у египтян. Если проанализировать архитектуру Египта того времени, можно чётко проследить соблюдение математической гармонии. Необычные свойства числовой зависимости стали причиной мистического отношения к золотому сечению:

• практически все живые организмы можно привести к принципу числовой зависимости. Например, тело человека, количество семечек в подсолнухе, структуру ДНК, произведения искусства и вирусную бактерию;
• данная зависимость чисел характерна только для биологических существ и кристаллов, все остальные неживые объекты природы крайне редко обладают золотой пропорцией;
• именно математическая пропорция в строении биологических объектов оказалась оптимальной для выживания.

Золотое сечение в природе, человеке, искусстве

Прежде, чем мы начнем, хотелось бы уточнить ряд неточностей. Во-первых, само определение золотого сечения в данном контексте не совсем верно. Дело в том, что само понятие «сечение» — это термин геометрический, обозначающий всегда плоскость, но никак не последовательность чисел Фибоначчи.

И, во-вторых, числовой ряд и соотношение одного к другому, конечно, превратили в некий трафарет, который можно накладывать на все, что кажется подозрительным, и очень радоваться, когда есть совпадения, но все же, здравый смысл терять не стоит.

Однако, «все смешалось в нашем королевстве» и одно стало синонимом другого. Так что в общем и целом, смысл от этого не потерялся. А теперь к делу.

Вы удивитесь, но золотое сечение, точнее пропорции максимально приближенные к нему, можно увидеть практически везде, даже в зеркале. Не верите? Давайте с этого и начнем.

Пропорции золотого сечения в человеке

Знаете, когда я училась рисовать, то нам объясняли, как проще строить лицо человека, его тело и прочее. Все надо рассчитывать, относительно чего-то другого.

Все, абсолютно все пропорционально: кости, наши пальцы, ладони, расстояния на лице, расстояние вытянутых рук по отношению к телу и так далее. Но даже это не все, внутреннее строение нашего организма, даже оно, приравнивается или почти приравнивается к золотой формуле сечения. Вот какие расстояния и пропорции:

• от плеч до макушки к размеру головы = 1:1.618

• от пупка до макушки к отрезку от плеч до макушки = 1:1.618

• от пупка до коленок и от коленок до ступней = 1:1.618

• от подбородка до крайней точки верхней губы и от нее до носа = 1:1.618

Разве это не удивительно!? Гармония в чистом виде, как внутри, так и снаружи. И именно поэтому, на каком-то подсознательном что-ли уровне, некоторые люди не кажутся нам красивыми, даже если у них крепкое подтянутое тело, бархатная кожа, красивые волосы, глаза и прочее и все остальное. Но, все равно, малейшее нарушений пропорций тела, и внешность уже слегка «режет глаза».

Короче говоря, чем красивее кажется нам человек, тем ближе его пропорции к идеальным. И это, кстати, не только к человеческому телу можно отнести.

Золотое сечение в природе и ее явлениях

Классическим примером золотого сечения в природе является раковина моллюска Nautilus pompilius и аммонита. Но это далеко не все, есть еще много примеров:

• в завитках человеческого уха мы можем увидеть золотую спираль;

• ее же (или приближенную к ней) в спиралях, по которым закручиваются галактики;

• и в молекуле ДНК;

• по ряду Фибоначчи устроен центр подсолнуха, растут шишки, середина цветов, ананас и многие другие плоды.

Друзья, примеров настолько много, что я просто оставлю тут видеоролик (он чуть ниже), чтобы не перегружать текстом статью. Потому что, если эту тему копать, то можно углубиться в такие дебри: еще древние греки доказывали, что Вселенная и, вообще, все пространство, — спланировано по принципу золотого сечения.

Вы удивитесь, но эти правила можно отыскать даже в звуке. Смотрите:

• Наивысшая точка звука, вызывающая боль и дискомфорт в наших ушах, равна 130 децибелам.

• Делим пропорцией 130 на число золотого сечения φ = 1,62 и получаем 80 децибел — звук человеческого крика.

• Продолжаем пропорционально делить и получаем, скажем так, нормальную громкость человеческой речи: 80 / φ = 50 децибел.

• Ну, а последний звук, который получим благодаря формуле – приятный звук шепота = 2,618.

По данному принципу можно определить оптимально-комфортное, минимальное и максимальное число температуры, давления, влажности. Я не проверяла, и не знаю, насколько эта теория верна, но, согласитесь, звучит впечатляюще.

Главное, только не увлекаться этим, ведь если мы хотим что-то в чем-то увидеть, то увидим, даже если этого там нет

Вот я, например, обратила внимание на дизайн PS4 и увидела там золотое сечение =) Впрочем, эта консоль настолько классная, что не удивлюсь, если дизайнер, и правда, что-то там мудрил

Золотое сечение в искусстве

Тоже очень большая и обширная тема, которую стоит рассмотреть отдельно. Тут лишь помечу несколько базовых моментов. Самое примечательное, что многие произведения искусства и архитектурные шедевры древности (и не только) сделаны, по принципам золотого сечения.

• Египетские и пирамиды Майя, Нотр-дам де Пари, греческий Парфенон и так далее.

• В музыкальных произведениях Моцарта, Шопена, Шуберта, Баха и прочих.

• В живописи (там это наглядно видно): все самые знаменитые картины известных художников сделаны с учетом правил золотого сечения.

• Эти принципы можно встретить и в стихах Пушкина, и в бюсте красавицы Нефертити.

• Даже сейчас правила золотой пропорции используются, например, в фотографии. Ну, и конечно, во всем остальном искусстве, включая кинематограф и дизайн.

https://youtube.com/watch?v=c3SVIQBXMnA

Золотое сечение в науке

Общее сопротивление этой бесконечной цепи равно Фr.

Золотое число возникает в разных задачах, в том числе в физике. Например, бесконечная электрическая цепь, приведенная на рисунке имеет общее сопротивление (между двумя левыми концами) Ф·r.

Отношение амплитуд колебаний и частот ~ Ф.

Существуют колебательные системы, физические характеристики которых (отношения частот, амплитуд и др.) пропорциональны золотому сечению. Самый простой пример — система из двух шариков, соединенных последовательно пружинами одинаковой жесткости (см. рисунок).

Полностью эти две задачи рассматривается в книге «В поисках пятого порядка», глава «Две простые задачки». Более сложные примеры на механические колебания и их обобщения рассматриваются в этой же книге, в главе «Обобщения одной простой задачи по механике». В книге приведено много примеров проявления и применения золотого сечения в различных областях наук — небесной механике, физике, геофизике, биофизике, физической химии, биологии, физиологии.

Золотое сечение сильно связано с симметрией пятого порядка, наиболее известными трехмерными представителями которой являются додекаэдр и икосаэдр. Можно сказать, что всюду, где в структуре проявляются додекаэдр, икосаэдр или их производные, там в описании будет появляться и золотое сечение. Например, в пространственных группировках из Бора: В-12, В-50, В-78, В-84, В-90, …, В-1708, имеющих икосаэдрическую симметрию.
Молекула воды, у которой угол расхождения связей Н-О равен 104.7 , то есть близок к 108 градусам (угол в правильном пятиугольнике), может соединяться в плоские и трехмерные структуры с симметрией пятого порядка. Так в разреженной плазме был обнаружен Н+(Н₂0)₂₁, который представляет из себя ион Н₃0+, окруженный 20 молекулами воды, расположенными в вершинах додекаэдра. В 80-х годах XX века были получены клатратные соединения, содержащие гексааквакомплекс кальция, окруженный 20 молекулами воды, расположенными в вершинах додекаэдра. Есть и клатратные модели воды, в которых обыкновенная вода отчасти состоит из молекул воды, соединенных в структуры с симметрией пятого порядка. Такие структуры могут состоять из 20, 57, 912 молекул воды.

Золотое сечение в физике

Последовательность чисел Фибоначчи и формула золотого сечения непосредственным образом затрагивает и сферу физики и физических законов:

«Представим две соприкоснувшиеся между собой стеклянные пластины. Теперь направим на них луч света. Часть луча пройдет сквозь стекло, другая часть поглотиться, оставшаяся же часть отразится от стекла. Произойдет явление «множественного отражения». Количество путей, которые проходит луч внутри стекла, прежде чем пройти и выйди сквозь стекло, зависит от количества лучей, который не прошли сквозь стекло, а подверглись отражению. Если подсчитать количество лучей, отразившихся от стекла и прошедших сквозь него, то опять же мы получим последовательность чисел Фибоначчи в соотношении 1:1.618.»

Строение всех встречающихся в природе живых организмов и неживых объектов, не имеющих никакой связи и подобия между собой, спланировано по определенной математической формуле. Это является самым ярким доказательством их осознанной сотворенности согласно некоему проекту, замыслу. Формула золотого сечения и золотые пропорции очень хорошо известны всем людям искусства, ибо это главные правила эстетики. Любое произведение искусства, спроектированное в точном соответствии с пропорциями золотого сечения, являет собой совершенную эстетическую форму.

Пропорции золотого сечения в материальном мире

В 1509 году Лука Пачоли написал книгу, которая называет число Ф «Божественной пропорцией», что было наглядно показано Леонардо да Винчи. Позже да Винчи назвал эту пропорцию золотым сечением. Оно использовалось для достижения баланса и красоты во многих картинах и скульптурах эпохи Возрождения.

Да Винчи сам использовал золотое сечение, чтобы определить все пропорции в «Тайной вечере», включая размеры стола, пропорции стен и деталей интерьера. Золотое сечение также появляется в «Витрувианском Человеке» да Винчи и «Мона Лизе». Считается, что золотое сечение использовали и другие великие художники, включая Микеланджело, Рафаэля, Рембрандта, Сьюрата и Сальвадора Дали.

Термин «фи» был придуман американским математиком Марком Барром в 1900-х годах. Ф продолжал применяться в математике и физике, в том числе в плитках Пенроуза 1970-х годов, которые позволяли мозаичным поверхностям иметь пятикратную симметрию. В 1980-х годах Ф появился в квазикристаллах – недавно открывшейся форме материи.

Фи — более чем загадочный и неясный термин в математике и физике. Он появляется вокруг нас в нашей повседневной жизни, даже в наших эстетических взглядах. Исследования показали, что когда испытуемые видят случайные лица, они считают наиболее привлекательными те, которые имеют четкие параллели с золотым сечением. Лица, оцененные как наиболее привлекательные, показывают золотые соотношения между шириной лица и шириной глаз, носа и бровей. Испытуемые не были математиками или физиками, знакомыми с правилом золотого сечения (они были просто среднестатистическими людьми), и оно вызвало инстинктивную реакцию.

Золотое сечение также проявляется во всех видах природы и науки. Ниже приведены примеры самых неожиданных мест, в которых можно его встретить.

• Цветочные лепестки. Количество лепестков на некоторых цветах соответствует последовательности Фибоначчи. С точки зрения теории Дарвина считается, что каждый лепесток помещается таким образом, чтобы обеспечить максимально возможное воздействие солнечного света и других факторов.
• Семенные головки. Семена цветка часто начинают произрастать в центре семенной головки и мигрируют наружу, заполняя свободное пространство. Например, семечки подсолнухов следуют этой схеме.
• Сосновые шишки. Семенные коробочки сосновых шишек наполнены семенами, которые растут спирально вверх, в противоположных направлениях. Количество шагов, которые делают спирали, как правило, соответствует числам Фибоначчи.
• Ветви дерева. То, как ветки дерева формируются или расщепляются, является примером последовательности Фибоначчи. Корневые системы и водоросли также придерживаются такого способа формирования.
• Раковины. Многие раковины, в том числе раковины улитки и раковины наутилуса, являются прекрасными примерами золотой спирали.
• Спиральные галактики. Млечный путь имеет несколько спиральных рукавов, каждый из которых имеет логарифмическую спираль примерно 12 градусов. Форма спирали идентична золотой спирали, а золотой прямоугольник можно нарисовать над любой спиральной галактикой.
• Ураганы. Внутреннее строение ураганов часто следует правилу золотой спирали.
• Пальцы руки человека. Каждый участок пальца от кончика основания до запястья больше, чем предыдущий, примерно на соотношение Ф.
• Тела человека и животных. Расстояние от пупка человека до пола и от макушки головы до пупка – это золотое сечение. Но человек не единственный пример золотого сечения в животном мире. Дельфины, морские звезды, морские ежи, муравьи и пчелы также демонстрируют эту пропорцию.
• Молекулы ДНК. Молекула ДНК имеет размеры 34 ангстрем на 21 ангстрем на каждом полном цикле спирали в виде сдвоенной спирали. В рядах Фибоначчи 34 и 21 являются последовательными числами.

Таким образом, примеров, где встречаются пропорции и соотношения, следующие правилу золотого сечения, более чем достаточно. Кроме перечисленных примеров, число «Фи» часто встречается в математике, физике, астрономии, биологии и иных сферах деятельности человека. Можно смело утверждать, что название «Божественное сечение» по праву присвоено числу Ф – видимо им руководствовался создатель, наполняя эту Вселенную всем живым и неживым.

Заключение

Принцип золотого сечения не является новым в архитектуре, поскольку в прежние времена здания строились не по типовым проектам, а с учетом индивидуальных особенностей будущих владельцев. Такие строения выглядят даже спустя многие года гармоничными и привлекательными. Интерьер, оформленный по правилам идеальной пропорции, позволяет грамотно использовать все площади.

Теперь вы сможете самостоятельно и правильно применить божественную гармонию математических цифр, планируя строительство дома или оформляя свой интерьер. Более того, интересную комбинацию цифр можно использовать и в экономике, и в расчете инвестиций и во всех деталях, с которыми соприкасается человек ежедневно.

Если у вас ещё остались вопросы, предлагаем посмотреть видео, в котором простыми словами разъяснен принцип действия золотого сечения:

Watch this video on YouTube

Предыдущая Новинки рынкаОт теории к практике: самостоятельная регулировка окон к зиме
Следующая Новинки рынкаБалкон и лоджия: в чём разница, о каких нюансах стоит знать, если вы решились на переделку?