Геометрическая фигура угол: определение угла, измерение углов, обозначения и примеры

Расчет уклона канализационной трубы: основные понятия

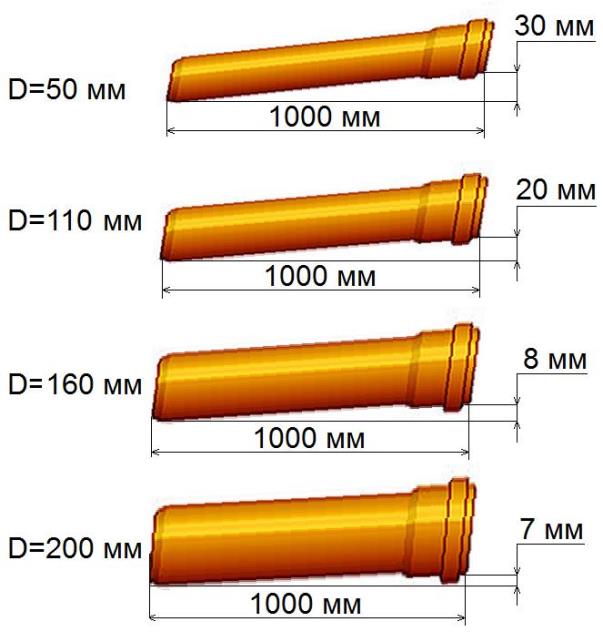
Если канализация самотечная, то ее эффективность транспортировки стоков за счет законов гравитации полностью зависит от угла наклона. Считается, что стоки должны двигаться по трубопроводу со скоростью 0,7-1 м/с. Только в этом случае поток способен удалить из системы твердые частицы. Чтобы сохранить показатель скорости потока, для каждого отдельного диаметра требуется рассчитать угол уклона канализационной трубы.

На первый взгляд может показаться, что угол должен измеряться в градусах. Но в строительных нормах и справочниках по устройству канализации этот параметр определен как десятичная дробь. Эти цифры отображают отношение снижения уровня к длине определенного участка трубопровода.

Например, на отрезке трубопровода длиной 5 м один его конец на 30 см ниже другого. В этом случае уклон канализационной трубы будет 0,30/5=0,06.

Формула — определение максимального, минимального значения

• V скорость движения потока жидкости (м/с);
• H наполнение трубопровода;
• d диаметр труб;
• К расчетный коэффициент наклона.

Чтобы определить коэффициент (наклон), можно подставить V=0,7-1, d- значение диаметра конкретного участка трубопровода, H=0,6хd (согласно строительным нормам и правилам). Получается, что для трубопровода с диаметром 100 мм на каждый метр требуется наклон в 2 см, с диаметром 50 мм — 3 см на каждый метр.

Из формулы видно, что скорость потока сточных вод напрямую зависит от угла наклона (коэффициента). Для оптимальной скорости необходим минимальный уклон канализационной трубы 0,02 и максимальный — 0,03. Если крен будет меньше, чем 0,02, крупные частицы осядут и образуют засор.

Если крен будет слишком большой, скорость увеличится, что тоже приведет к образованию осадков, так как вода будет уходить слишком быстро, не успевая унести с собой тяжелые частицы стоков. Повышение скорости потока может привести так же к срыву сифонов и запоров.

Необходимые нормы в квартире

При устройстве канализации нет необходимости использовать для расчетов формулу. Существуют таблица, в которой определены наклоны для всех отводов от сантехнических приборов.

Оптимальный уклон канализационных труб в квартире
Прибор	Диаметр слива (мм)	Расстояние до сифона (см)	Наклон
Ванна	40	100-130	0.033
Душ	40	150-170	0,029
Унитаз	100	Не более 600	0,05
Раковина	40	До 80	0,08
Биде	30-40	70-100	0,05
Мойка	30-40	130-150	0,02
Комбинированный слив для ванны, мойки и душа	50	170-230	0,029
Стояк	100
Отвод от стояка	65-754

Каждый участок системы канализации в квартире должен иметь на конце сифон в виде прибора или изгиба, чтобы в помещения не попадали неприятные запахи. Чтобы определить необходимые значения, важен принцип золотой середины — 1,5-2.5 см на один метр. Этого вполне достаточно для квартиры или загородного дома. Применение формул необходимо при строительстве больших объектов с максимальным объемом сточных вод.

К тому же, для бытовой канализации формулу трудно использовать, так как постоянного потока нет

Тут лучше обратить внимание на другой показатель — способность к самоочищению (удалению твердых частиц)

Так как бытовые стоки содержат отходы с различным весом, то для тяжелых составляющих определяющим фактором является скорость потока, для плавучих — наполнение диаметра системы. Определяя правильный уклон, следует учитывать, что он будет различный на каждом отдельном участке.

Зачем измеряют угол уклона покрытия и от каких факторов зависит эта величина

Угол ската крыши — это геометрическое образование пересечения двух плоскостей. Под ними подразумевается горизонтальная плоскость и аналогичная поверхность ската.

Итак, зачем измерять угол крыши:

1. Измерение строительного азимута, в первую очередь, позволяет «прикинуть» целесообразность устройства крыши с учетом выбранного материала кровли, климатических особенностей, предназначения чердака и конструкции самого навеса.
2. К тому же, после проведения расчетов можно не только рационализировать предстоящие финансовые расходы, но и удостовериться в правильности и надежности проектирования, которое не повлечет за собой убытки из-за протеканий, обвалов, трещин стропил и прочих казусов.
3. Уклон крыши принимается в зависимости от двух параметров — первое касается погодных условий и объемов осадков, а второе характеризуется спецификой типа кровли. Соответственно, когда речь идет о северных и снежных районах, тогда будущей крыше придется бороться с приличными нагрузками. С подобными сложностями не по наслышке знакомы жители горных областей.
4. Некоторым крышам приходится выдерживать снежные покровы по 6-8 месяцев в году. В сложившихся условиях владельцам заснеженных домиков существенно упростили жизнь более крутая степень наклона. В свою очередь такие строительные пеленги позволяют вальме рационально бороться с осадками и их последствиями в виде талой воды. Также с таким подходом возрастают размеры полезной площади.

ОБРАТИТЕ ВНИМАНИЕ!
Когда уклон установлен на отметке 45 градусов и выше, расчет снеговой нагрузки уже не принимают во внимание, поскольку такая кровля является «самоочищающейся».

Само собой, не все так хорошо с острым румбом, ведь увеличивая склон, пропорционально растет необходимость в дополнительных объемах как кровельных материалов, так и элементов конструкции. Также становится актуальным вопрос повышения стойкости несущих деталей.

Не менее важным при расчете уклона является специфика материала, который будет завершать структуру навеса с внешней стороны. Ни для кого ни секрет, что каждый тип верхнего элемента крова отличается эксплуатационными свойствами и стоимостью.

В то же время могут быть предусмотрены нюансы, которые характерны исключительно для такого вида верхнего слоя крыши. К примеру, возможно потребуется настилание дополнительных слоев, либо понадобится большие расходы на тепло- и гидроизоляцию.

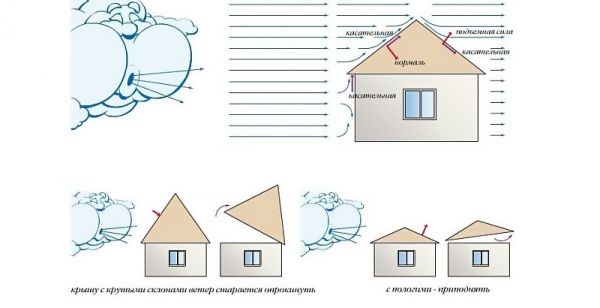
Угол уклона зависит от розы ветров

Пожалуй, третьим по значимости фактором, от которого зависит рассчитываемый склон — это установление эксплуатируемого или не эксплуатируемого статуса. Не эксплуатируемая поверхность предусматривает исключение пространства на стыке перекрытия и внешней защитной конструкции.

Визуально трактовка понятия выглядит гораздо проще, поскольку при виде плоских вальм или при наличии небольшого уклона (в интервале 2-7%), сразу становится понятно, почему она получила такое название. Эксплуатируемая мансарда указывает на наличие чердачного пространства.

Как учитывается угол наклона при расчете стропильной системы

Расчет состоит из нескольких этапов, каждый имеет свои требования и учитывает определенные условия.

Шаг 1. Расчет нагрузки на погонный метр стропильной ноги. Мы уже упоминали, что от показателей угла наклона во многом зависит распределение усилий. Стропильная нога условно принимается за балку с двумя или несколькими точками упора, от угла наклона зависят значения продольных и поперечных усилий. Каждое отдельное усилие определяется после построения эпюры как катет прямоугольного треугольника. При этом угол наклона играет важную роль, именно его значение синусов, косинусов и тангенсов используются для определения нагрузок.

Разложение нагрузки на стропила на вертикальную и горизонтальную составляющие

Для расчета суммарной нагрузки нужно расстояние между точками упора стропильных ног умножить на расстояние между стропильными ногами и на суммарную нагрузку. С учетом значения этой силы строится эпюра. Но на практике расчеты по эпюрам не нужно делать, в СНиПе есть таблицы с готовыми данными.

Шаг 2. Определение площади сечения пиломатериалов, используемых для изготовления стропильных ног. Это очень важный этап расчетов. Исходные данные надо брать из ГОСТа 24454-80, прочность материалов дана с учетом вида древесины. Для стропильных ног универсальными считаются доски толщиной 50 мм, ширина подбирается в зависимости от ранее рассчитанных нагрузок.

Таблица размеров и других параметров стропил

С учетом величины угла наклона по формулам рассчитывается ширина доски, исходные данные – толщина стропилины.

Оптимальный шаг и сечение стропил под металлочерепицу

Имейте в виду, что максимальная длина стропилины – это не общая длина, а расстояние между соседними упорами. Упорами смогут быть как вертикальные стойки, так и раскосы или различные стяжки.

Элементы стропильных систем

Еще раз напоминаем, что во время расчетов параметров стропилины надо брать максимальное расстояние, одна нога может иметь несколько опорных точек. Этот общий подход используется для расчетов на прочность любых конструкций, всегда берется самое слабое и наиболее нагруженное место. Только так можно с достаточным запасом прочности и устойчивости спроектировать стропильную систему.

Во время непосредственного строительства кровельщики могут увеличивать количество упоров или уменьшать расстояние между ними и за счет этого дополнительно повышать устойчивость конструкции. Но категорически запрещается уменьшать количество опорных элементов или увеличивать расстояние между опорными точками. Такие действия обязательно приведут к деформации крыши. Она может случиться как сразу после окончания кровельных работ, так и через несколько лет после начала эксплуатации здания.

Монтаж стропильной системы двухскатной крыши должен производиться по проекту

На основании расчетов определяется минимальная ширина доски для стропил при толщине 50 мм с учетом оптимального угла наклона скатов. Это значение никогда не будет стандартным, окончательно выбирать доску нужно с запасом по ширине. К примеру, если у вас получилось 90 мм, то доску надо брать 100 мм, если 120 мм, то ширина стропильной ноги должна быть 150 мм. За счет такого подхода компенсируется возможное уменьшение прочности пиломатериалов. Дело в том, что в мире не существует двух досок с полностью одинаковыми свойствами. На механическую прочность оказывает влияние огромное количество факторов, не поддающихся расчетам. Никто не знает, сколько именно трещин или сучков будет иметь доска на расчетном участке, есть ли заболонь или иные пороки развития древесины, как она сушилась, какие допуски по толщине и ширине и т. д.

Еще один момент – одна и та же доска изменяется свою прочность в зависимости от влажности, температуры наружного воздуха и времени эксплуатации.

Деформация древесины

Мера усадки и деформации симметричной доски зависит от распиловки

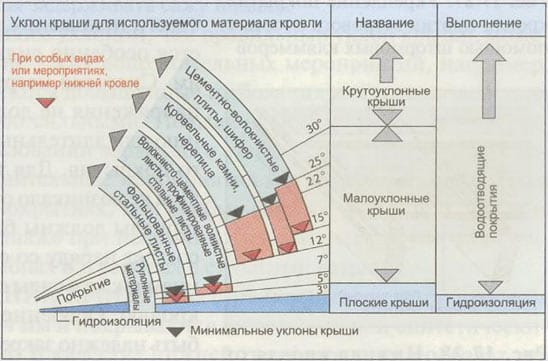
Как величина уклона зависит от используемого материала

Кровля загородного дома или хозяйской постройки может иметь низкие или отвесные скаты. Во время проектирования этой конструкции необходимо рассчитать сечение стропил и расстояние между ними. Как определить угол наклона для разных кровельных материалов, пытаются понять многие, но эти значения давно уже вычислены.

Во время монтажа рулонных гидроизоляционных материалов, когда рубероид укладывается в два слоя, наклон покрытия не должен превышать 15 градусов. Многие хотели бы знать, как определить угол наклона крыши в градусах если она покрыта тремя слоями гибкой черепицы. В данном случае описываемый показатель может меняться от 2 до 5 градусов.

Обратите внимание на следующие нюансы устройства:

• Наплавляемый рубероид рекомендован к использованию при величине уклона до 25˚ в два слоя, от 0 до 10˚ – в три слоя. При наличии крыши с уклоном 10…25 градусов можно уложить один слой рулонных материалов, но лицевая поверхность такого покрытия должна иметь специальный защитный слой.
• Асбестоцементные листы используются на кровлях, имеющих уклон до 26˚.
• Минимальный уклон для натуральной черепицы составляет 33 градуса;
• Профлист или металлочерепица – 29 градусов и больше.

Расход кровельных изделий тоже зависит от рассматриваемого параметра. так конструкции с небольшими уклонами стоят гораздо дешевле аналогов, имеющих угол больше 45 градусов.

Факторы, которые определяют угол наклона

Известно, что максимальный угол кровли с 1 скатом составляет 20 градусов. Какой выбрать и как рассчитать угол наклона крыши? Чтобы найти ответ на этот вопрос, необходимо учитывать такие факторы:

• Назначения сооружения;
• Климат местности;
• Материал покрытия.

Если количество скатов вы хотите увеличить, то ваше сооружение будет иметь дополнительное пространство – чердак. На этом этапе вам нужно определиться с его назначением. Допустим, если чердак не будет жилым, а его будут использовать только для хранения ненужных вещей, то его высота может быть минимальной. Все с точностью до наоборот касается жилого чердака.

Фактор местности

Что касается местности, то в ветреных регионах лучше сооружать крыши с минимальным углом наклона. При большом порыве ветра нагрузка на конструкцию значительно возрастает, а такой тип крыши позволит свести ее к минимуму. Такую же кровлю лучше соорудить в местности, где объем атмосферных осадков минимален.

Если же объем осадков превышает норму, то угол наклона должен быть, наоборот, большим. Так, снег и дождь не будут задерживаться на поверхности, а значит, нагрузка будет минимальной.

Прежде чем выбрать угол наклона кровли, следует рассмотреть внимательно каждый фактор, описанный выше. Сегодня можно встретить кровли разных конфигураций. Многие специалисты утверждают, что в основном сооружают кровли с углом от 20 градусов до 40. Это оптимальный вариант, который позволяет использовать различные материалы. Рассмотрим, как правильно провести расчет угла наклона крыши.

Существует множество советов, которые способствуют правильному выбору материала для покрытия крыши. На односкатных кровлях можно использовать каменную крошку, покрыв нею основание. Если наклон больше 10 градусов, то необходимо использовать надежные гидроизоляционные материалы, основой которых является битум.

Для рулонного материала необходимо использовать дополнительный слой гидроизоляции

Используя профилированный лист и шифер в качестве кровельного материала, следует обратить внимание на стыки. Их дополнительно герметизируют

Зависимость угла от места строительства

В регионах с постоянными сильными ветрами необходимо делать уклон минимальным. В связи с этим нагрузка от потоков воздуха на кровлю будет небольшой. Высокие крыши страдают от ветра гораздо больше, чем низкие. Нельзя сказать, что ветер не срывает покрытие с крыш, имеющих небольшой уклон. Далее узнаем, как найти угол наклона кровли для зданий, построенных в регионах с постоянными ветрами:

• При небольшой интенсивности воздушных потоков уклон имеет значение 34-40 градусов;
• При наличии сильных ветров этот показатель уменьшают до 15…25 градусов.

В местности с большим количеством атмосферных осадков наклон желательно увеличивать до параметров в 60˚. Такой уклон позволит быстро выводить снег и воду за пределы покрытия. Уклон крыши обычно меняется в диапазоне 9…60˚, но самыми распространёнными вариантами уклона считается диапазон 19…44 градуса.

Совет 3 Как вычислить уклон

Если вам надобно вычислить уклон ската крыши либо уклон дороги, ваши действия будут различными, правда тезис расчета идентичен. Выбирать формулу для расчета уклон а следует в зависимости от того, в каких единицах необходимо получить итог.

Инструкция

1. В первую очередь реально либо мысленно постройте прямоугольный треугольник, в котором одной из сторон будет опущенный на землю перпендикуляр. Дабы возвести такой треугольник на участке земли либо дороге, воспользуйтесь нивелиром. Определите высоту в 2-х точках измеряемого объекта над ярусом моря, а также расстояние между ними.

2. Если надобно обнаружить уклон небольшого объекта, расположенного на земле, возьмите ровную доску либо и, применяя уровнемер, расположите ее сурово горизонтально между двумя точками. В нижней точке под нее придется подложить подручные средства, скажем, кирпичи. Померяйте рулеткой длину доски и высоту кирпичей.

3. Дабы обнаружить уклон ската крыши, зайдите на чердак и от определенной точки ската опустите вниз нить с грузом, до самого пола. Измерьте длину нити и расстояние от опущенного груза до пересечения ската с полом чердака. Методы измерения могут быть самыми различными, вплотную до фотографирования объекта и измерения сторон на фотографии – ваша цель при этом узнать длину 2-х катетов в полученном прямоугольном треугольнике.

4. Если у вас есть довольно подробная карта физическая карта местности, посчитайте уклон с ее подмогой. Для этого подметьте крайние точки и посмотрите, какие обозначения высоты там подмечены, обнаружьте между ними разницу. Измерьте расстояния между точками и при помощи указанного масштаба посчитайте настоящее расстояние

Обратите внимание, все расстояние обязаны быть измерены в одних и тех же единицах, скажем, только в метрах либо только в сантиметрах

5. Поделите противолежащий катет (вертикальное расстояние) на прилежащий (расстояние между точками). Если вам необходимо получить уклон в процентах, умножьте полученное число на 100%. Дабы получить уклон в промилле, умножьте итог деления на 1000‰.

6. Если вам нужно получить уклон в градусах, воспользуйтесь тем, что полученный при делении катетов итог – тангенс угла наклона. Посчитайте его арктангенс при помощи инженерного калькулятора (механического либо онлайн). В итоге вы получите значение уклон а в градусах.

Виды конструкционного решения крыш

Существует 4 вида конструкционного решения крыши, поэтому в зависимости от уклона кровли, она может быть:

• плоской. В действительности абсолютно плоских перекрытий зданий не строят, поскольку на них постоянно будет задерживаться влага от дождя или растаявшего снега. Уклон крыши не может быть меньше 3-х градусов (подробнее: «Виды кровли для крыши — классификация «);
• скатной;
• пологой;
• высокой.

Поскольку величину уклона измеряют как в процентах, так и в градусах, имеется специальная таблица, согласно которой можно определить соотношение между данными величинами. Например: угол наклона ската равен 30 градусов, тогда уклон кровли в процентах составит 57,7%.

Как узнать уклон дороги отчёт, 2017 год

Уклон 12%, сколько это в градусах? | Автор топика: Артем

Помогите, пожалуйста, разобраться: что такое уклон 12%? Сколько это будет в градусах и есть ли вообще разница в процентах от градусов? Заранее благодарю.

Евгений Означает перепад высот на 12 м по вертикали на 100 м пути..

Роман 12% от 90 градусов.

Илья 360 — 100%, дальше сам

Артём разница есть конечно: 12%=10,8 градусов

Иван примерно 7 град

Ярослав сколько процентов столько и градусов. а то понимешь градусы они и в температуре тоже градусы и в спиртном градусы, а то дорожный знак может в заблуждение ввести.)))

Денис уклон 12% — это отношение высоты к длине основания. Поэтому уклон 100% — это 45 градусов, а 12% — это примерно 6,85 градусов, он же тангенс

Петр проценты это возвышение, метров вертикальных на сто метров горизонтальных решите как прямиоугольный треугольник отношение сторон это тангенс угла. извлечь арктангенс получите угол

Константин Уклон дороги — относительное превышение одной точки продольного Григорий профиля дороги над другой, определяемое как отношение превышения к горизонтальному расстоянию между двумя точками. Уклон 10% Это отношение высоты подъёма в 10 метров к горизонтальной проекции дороги длинной 100метров. В геометрическом смысле — это тангенс угла подъёма дороги. Чтобы перевести уклон из процентов в градусы надо уклон дороги в процентах разделить на100 и полученную велину посмотреть в таблице Брадиса раздел Тангенсы.

Для уклона 10% угол уклона в процентах будет примерно tgВалерий -0.105 Шесть градусов. Для уклона 100% угол наклона 45 градусов.

Михаил Это надо понимать также, как говорят: скидка цен на товары 40%, спрашивается от двух милионов скидывают или от трёх, а другой спрашивает, с какого этажа скидывают с пятого или с девятого?

Леонид уклон измеряется в промилле и имеет отношение длинны от высоты. 1 промилле равен 1 метру в высоту на 1000 метров длины все ответы из википедии. я окончил автодор на фак. строительство дорог.

Степан Это 6град. 50′ 33.98″ или 6.84град. Но это неудобно. Считайте, так, как предлагает выше Виктор. Это удобно.

Помогите, пожалуйста, разобраться: что такое уклон 12%? Сколько это будет в градусах и есть ли вообще разница в процентах от градусов? Заранее благодарю.

Никита Крутизну подъемов и спусков дорог называют уклоном. Величину уклона выражают в процентах и определяют по формуле:

i = Артём * 100

где h — высота подъема или спуска; L — длина подъема или спуска.

Уклон, равный 1%, обозначает подъем или спуск на 1 м на каждые 100 м дороги. Наибольшие продольные уклоны на автомобильных дорогах Poccuu не превышают 6 — 7% на равнинной и холмистой местности и 9 — 10% в горах. Конвенция о дорожных знаках и сигналах Виктор Договаривающиеся стороны, признавая, что единообразие дорожных знаков, сигналов и обозначений и разметки дорог в международном плане необходимо для облегчения международного дорожного движения и повышения безопасности на дорогах.

Станислав Курсовик Лепиш?, Удачи, а то ко Мне в Часть Попадёшь!

Денис На железной дороге величина уклона измеряется не в процентах, а в промилле. Т. е. «одна тысячная» уклона — спуск на 1 метр на 1 км расстояния. На автодорогах — так же, только измеряется в процентах. Т. е. на 100 м. расстояния.

Детский город из бумаги

Jul 7, 2014 — Хотите создать огромный город из бумаги прямо у себя на столе? … Для придания городу подобающего вида можно сделать различные здания и … Для того, чтобы построить автомобильную или железную дорогу …

tomnosti.info

Геометрические фигуры с развернутыми углами

В геометрии производя некоторые манипуляции с развернутыми углами, можно получить новые фигуры. К примеру, если такую геометрическую фигуру разделить лучом на два угла, то полученные углы называют смежными. Такие элементы изображены на рисунке.

∠ABD  в данном случае является развернутым углом, а ВС представляет собой луч. Таким образом, углы ∠ABС и ∠CBD — смежные углы.

С помощью биссектрисы можно разделить представленную фигуру на два прямых угла. Наглядно данный метод получения геометрических фигур продемонстрирован на рисунке.

Так, согласно изображению, KF является биссектрисой развернутого ∠MKP. Полученные углы, ∠MKF и ∠FKP представляют собой прямые углы.

Как материал может повлиять на наклон крыши?

Крыша представляет собой достаточно сложное конструктивное сооружение, состоящее из стропильной системы и нескольких слоев кровельных материалов. Каждый, из них может использоваться только при определенных значениях угла наклона крыши.

К универсальным материалам, в отношении этого показателя, можно отнести разве, что мембранные покрытия. Их использование не ограничивается углом наклона.

Например, использование наборных материалов на крутых скатах нежелательно, т.к. они могут съезжать под влиянием собственного веса. При небольшом наклоне эти материалы, напротив, будут создавать дополнительную нагрузку на стропильную систему.

Для битумной черепицы угол наклона определяет плотность обрешетки. При пологих скатах ее делают максимально плотной с целью придать дополнительную прочность кровле. Сама мягкая кровля имеет значительный вес, который может существенно увеличиваться при формировании снежного покрова. Крутые скаты позволяют сделать менее плотную обрешетку с шагом в 45 см.

Пример расчёта

А теперь ознакомимся, как рассчитать угол наклона крыши на конкретном примере. Для начала необходимо узнать высоту конька по отношению к основанию. Этот параметр зависит от предназначения чердака. Если это помещение будет использоваться в качестве мансарды, то нам понадобится ещё одна величина – длина фронтона или основания.

Как измерить угол наклона, если высота от основания кровли до конька составляет 1,8 метра, а длина фронтона принимается кратной 6 метрам. Для начала необходимо разделить «подошву треугольника» на две части, а затем вычисляют синус угла по теореме Пифагора.

В нашем случае, это значение синуса угла, который находится из соотношения прилежащей стороны к противолежащей. Сначала делим треугольник на две равные части 6/2=3. Теперь вычисляем синус нужного угла 3/1,8= 1,6. Заглядываем в таблицу Брадиса и видим, что это значение соответствует углу в 59 градусов.

Советуем почитать:

• Каким должен быть угол наклона кровли из металлочерепицы;
• Определение угла наклона односкатной кровли;
• Минимальный уклон для кровли из профнастила

https://youtube.com/watch?v=fZ2cD9j-k98

https://youtube.com/watch?v=fOlIW8FXVP8

Теорема Пифагора

Теорема основана на утверждении, что у прямоугольного треугольника сумма квадратов длин катетов равна
квадрату длины гипотенузы. В виде формулы записывается это так:

a²+b²=c²

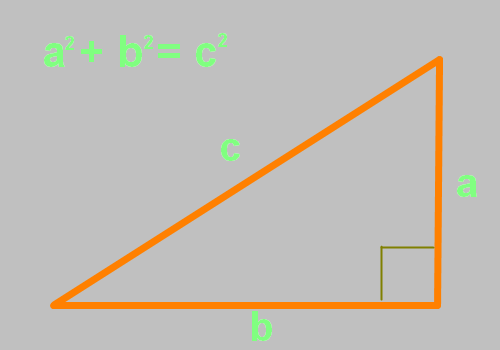
Стороны a и b — катеты, между которыми угол равен ровно 90 градусов. Следовательно, сторона c — гипотенуза.
Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную. А следовательно можем
размечать прямые углы, а также проверять их.

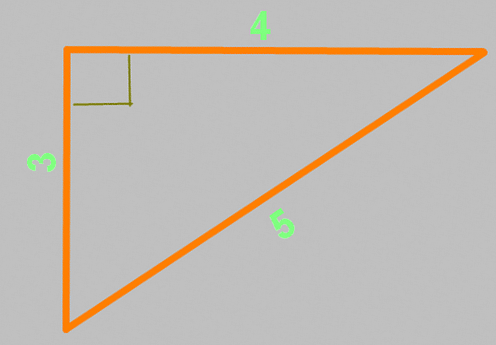
Теорема Пифагора известна еще под названием «египетский треугольник»

Это треугольник со сторонами 3, 4 и 5,
причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 — ровно девяносто градусов

Проверим
данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 — все
сходится!

А теперь применим теорему на практике.

Как можно вычислить прямой угол?

Итак, в этой статье будет описан принцип 3-4-5 при определении угла в 90 градусов. Ничего сложного в этом нет. Потребуется просто лишь чуть пораскинуть мозгами и вникнуть во все расчёты, которые смогут помочь в проверке угла.

Итак, нужно обозначить следующие шаги:

1. Для начала стоит разобраться в том, почему принцип так обозначен — 3-4-5. Это не просто набор цифр, это величина сторон прямоугольного треугольника. Теорема Пифагора гласит: квадрат гипотенузы равен сумме квадратов катетов. Цифры 3-4-5 очень подходят для проверки этого простого правила геометрии: 3*3+4*4=5*5, то есть 9+16=25. Именно эти цифры и будут использоваться в дальнейших вычислениях;
2. Итак, потребуется для начала отмерить 3 метра от угла вдоль одной из стен. Тут следует отметить, что 3 метра — предпочтительная длина замера, но в том случае, если комната маленькая, можно отметить всего 30 сантиметров. В месте замера нужно сделать отметку;
3. В принципе, можно использовать и другие цифры, но рекомендуется в любом случае использовать пропорционально увеличенные числа, например: 9-12-15 или же 30-40-50;
4. После проделанного предварительного замера нужно отмерить 4 метра вдоль другой стены, тоже от угла. Ну или соответственно 40 сантиметров, если комната маленькая. Нужно сделать отметку;
5. Теперь остаётся сделать последнее действие, по которому уже можно судить прямой угол или нет. От измеряющего потребуется измерить расстояние между сделанными отметками. По полученным данным можно будет сделать определённые выводы:
   • Если расстояние между отметками будет равняться 5 метрам ровно, это будет означать, что угол является прямым;
   • В том случае, если измеренное расстояние будет равняться меньше 5 метров, угол будет меньше, чем 90 градусов;
   • Ну и, наконец, величина угла будет составлять больше 90 градусов, если полученная величина замера будет равняться больше 5 метров.

Определение уклона при строительных работах

Специалисты, производящие кровельные работы, очень часто сталкиваются с необходимостью измерять уклоны крыш. Знание этих параметров позволяет выбрать тип материалов, которые будут использоваться, свериться с рекомендуемыми значениями для строений, выбрать метод ведения кровельных работ.

Чтобы не производить сложные математические расчеты каждый раз, был разработан специальный инструмент, который называется уклономер. Это приспособление устроено довольно просто. На рейку крепится специальная рамка, внутри которой закрепляется маятник, он имеет грузик и указатель. Рейку устанавливают в горизонтальном положении на измеряемом участке кровли и по указателю определяют на шкале численное значение уклона.

В случае, когда известно значение уклона крыши в градусах, перевести его в проценты можно воспользовавшись специальными таблицами. В них уже прописаны процентные значения для каждого угла от одного до сорока пяти градусов.

Советы в статье «Виды укладки ламината» здесь .

Как запилить стропила под нужным углом и нужных размеров смотрим в видео:

Полезно вспомнить

Треугольник

Треугольник
прямолинейный, часть плоскости, ограниченная тремя отрезками прямых (стороны Треугольника (в геометрии)), имеющими попарно по одному общему концу (вершины Треугольника (в геометрии)). Треугольник, у которого длины всех сторон равны, называется равносторонним
, или правильным
, Треугольник с двумя равными сторонами — равнобедренным
. Треугольник называется остроугольным
, если все углы его острые; прямоугольным
— если один из его углов прямой; тупоугольным
— если один из его углов тупой. Более одного прямого или тупого угла Треугольник (в геометрии) иметь не может, так как сумма всех трёх углов равна двум прямым углам (180° или, в радианах, p). Площадь Треугольник (в геометрии) равна ah/2, где а — любая из сторон Треугольника, принимаемая за его основание, a h — соответствующая высота. Стороны Треугольника подчинены условию: длина каждой из них меньше суммы и больше разности длин двух других сторон.

Треугольник
— простейший многоугольник , имеющий 3 вершины (угла) и 3 стороны; часть плоскости, ограниченная тремя точками, и тремя отрезками, попарно соединяющими эти точки.

• Трём точкам пространства, не лежащим на одной прямой, соответствует одна и только одна плоскость.
• Любой многоугольник можно разбить на треугольники — этот процесс называется триангуляция
  .
• Существует раздел математики, целиком посвящённый изучению закономерностей треугольников — Тригонометрия
  .

Типы треугольников

По виду углов

Поскольку сумма углов треугольника равна 180°, то не менее двух углов в треугольнике должны быть острыми (меньшими 90°). Выделяют следующие виды треугольников:

• Если все углы треугольника острые, то треугольник называется остроугольным;
• Если один из углов треугольника тупой (больше 90°), то треугольник называется тупоугольным;
• Если один из углов треугольника прямой (равен 90°), то треугольник называется прямоугольным. Две стороны, образующие прямой угол, называются катетами, а сторона, противолежащая прямому углу, называется гипотенузой.

По числу равных сторон

• Разносторонним называется треугольник, у которого длины трёх сторон попарно различны.
• Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, третья сторона называется основанием. В равнобедренном треугольнике углы при основании равны. Высота, медиана и биссектриса равнобедренного треугольника, опущенные на основание, совпадают.
• Равносторонним называется треугольник, у которого все три стороны равны. В равностороннем треугольнике все углы равны 60°, а центры вписанной и описанной окружностей совпадают.

Как разметить прямой угол рулеткой

Разметка может основываться как на общей теореме Пифагора, так и на принципе «египетского треугольника». Однако
это только в теории линии просто чертятся на бумаге, «ловить» же все выбранные размеры растянутыми шнурами или
линиями на полу — задача посложнее.

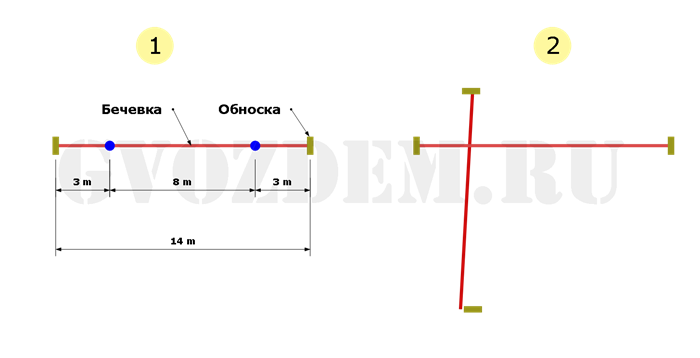
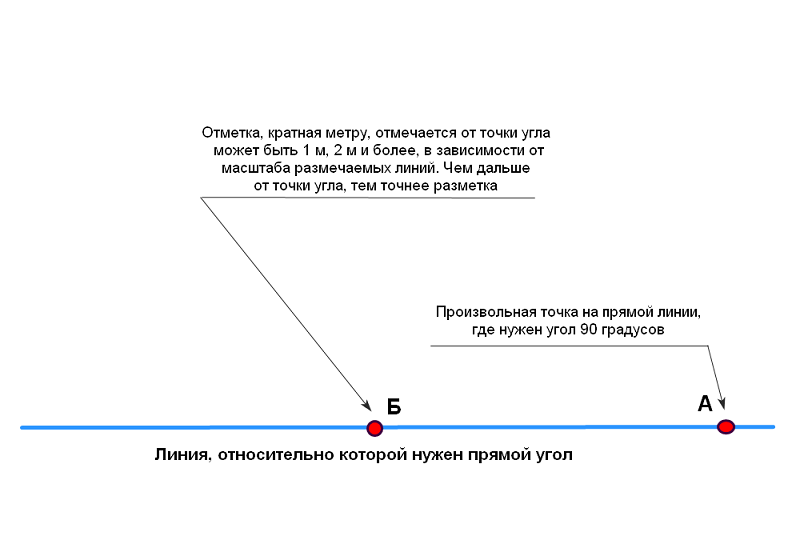
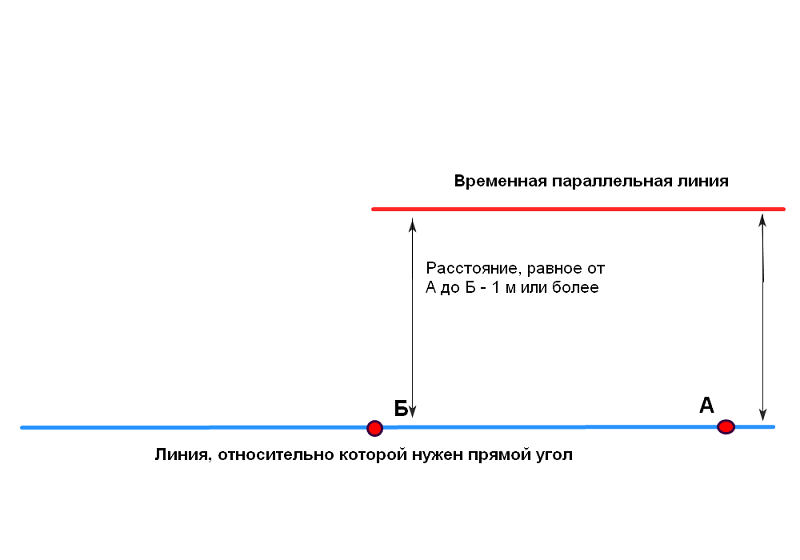
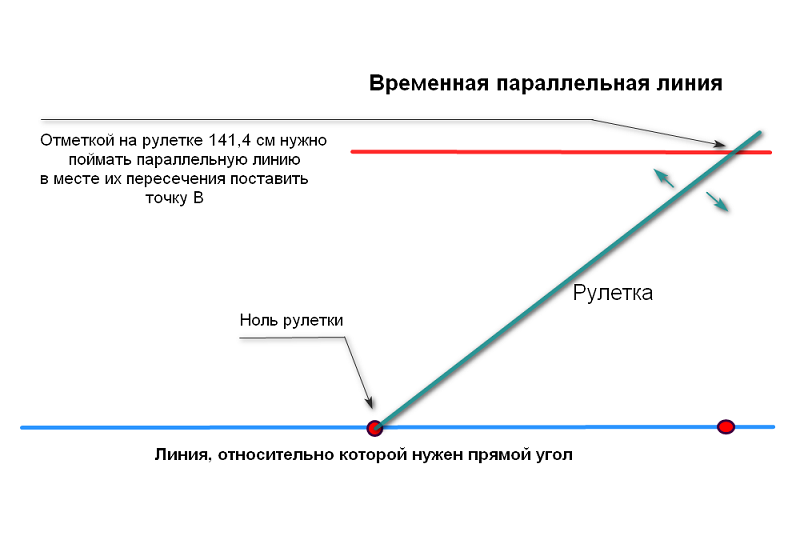
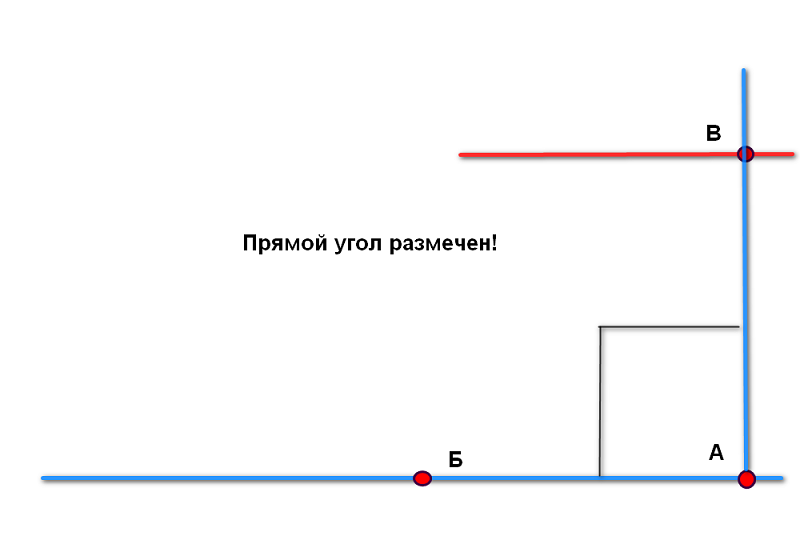
Поэтому я предлагаю упрощенный способ, основанный на диагонали 141,4 см. у треугольника со сторонами 100 см. Вся
последовательность разметки изображена на картинках ниже

Важно не забывать: диагональ 141,4 см. нужно умножать на
количество метров в отрезке А-Б

Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах.
Картинки увеличиваются по клику!

Нахождение угла между векторами

Как правило, угол между \( \overrightarrow a\) и \(\overrightarrow b\) можно найти с помощью скалярного произведения или теоремы косинусов для треугольника, который был построен на основе двух этих направляющих.

Определение

Скалярное произведение — это число, которое равно произведению двух направляющих на косинус угла между ними.

Формула скалярного произведения:

\(\left(\overrightarrow a;\overrightarrow b\right)=\left|\overrightarrow a\right|\times\left|\overrightarrow b\right|\times\cos\left(\widehat{\overrightarrow a;\overrightarrow b}\right)\)

1. Если α — острый, то СП (скалярное произведение) будет положительным числом (cos острого угла — положительное число).
2. Если векторы имеют общую направленность, то есть угол между ними равен \(0^\circ\), а косинус — 1, то СП будет тоже положительным.
3. Если α — тупой, то скалярное произведение будет отрицательным (cos тупого угла — отрицательное число).
4. Если α равен \(180^\circ\), то есть векторы противоположно направлены, то СП тоже отрицательно, потому что cos данного угла равен 1.
5. Если α — прямой, то СП равно 0, так как косинус \(90^\circ\) равен 0.

В случае, если \overrightarrow a и \overrightarrow b не нулевые, можно найти косинус α между ними, опираясь на формулу:

\(\cos\left(\widehat{\overrightarrow a;\overrightarrow b}\right)=\frac{\left(\overrightarrow a;\overrightarrow b\right)}{\left|\overrightarrow a\right|\times\left|\overrightarrow b\right|}\)

Конструктивные особенности крыши в зависимости от угла наклона

Если в проекте дан уклон крыши, то рассчитать ее высоту не составит труда. А этот параметр – один из самых важных, потому что он определяет высоту конька. Этот элемент кровельной конструкции – точка отправления в сооружении крыши в целом. Потому что при строительстве сначала выставляют уровень расположения конька, и уже под него режут пиломатериал: опорные стойки. Отсюда же рассчитывают длину стропильных ног.

Сложность расчета заключается в том, что не все помнят тригонометрию, формулы которой используются для расчетов длин элементов кровельного сооружения. В основе формул лежат тригонометрические функции: синус, косинус, тангенс, катангенс.

К примеру, как определить высоту конька (соответственно и крыши) через синус и тангенс:

sin α = H/S, где «S» – это длина ската. Соответственно высота конька будет равна: Н=S x sin α.

tg α = H / L , то есть Н= l x tg α

Точно также можно определить длину ската, или, зная оба параметра, можно рассчитать угол наклона крыши. Все параметры конструкции взаимосвязаны, так что, зная два из них, можно определить третий.

Кстати, определяя параметры крыши, можно обойтись и без угла наклона. Для этого используется формула Пифагора. Вот ее формула:

S2= H2+ L2

Меняя местами значения, находится необходимая величина.

У Вас может возникнуть вопрос, связанный со значением величин тригонометрических функций. Они в свободном доступе есть, но чтобы Вы их не искали на просторах интернета и не тратили свое время, предлагаем таблицу:

Значения тригонометрических функций от величины углаИсточник remont-kvartiri.livejournal.com

Добавим, что тригонометрические функции упрощают проведения расчетов кровельных конструкций. Если правильно ими пользоваться и уметь набрасывать на бумаге эскизы крыш (имея воображение в плане конструктивного расположения ее элементов), то можно легко рассчитать размеры каждого элемента.

Это касается не только одно- или двускатных сооружений. Также легко можно будет рассчитать и элементы вальмовых или мансардных крыш. Просто придется разбить их сложные конструкции на простые.